Additionstheorem mithilfe des Skalarprodukts
# Problem
Wir wollen beweisen, dass das Additionstheorem $$\cos(\theta_{1}+\theta_{2})=\cos\theta_{1}\cos\theta_{2}-\sin\theta_{1}\sin\theta_{2}$$ gilt, indem wir das Skalarprodukt der beiden unten abgebildeten Vektoren $\vec{v_1}$ und $\vec{v_2}$ betrachten. Die Winkel $\theta_{1}$ und $\theta_{2}$ sind dabei diejenigen Winkel, die die Vektoren $\vec{v_1}$ und $\vec{v_2}$ jeweils mit der $x$-Achse einschließen.
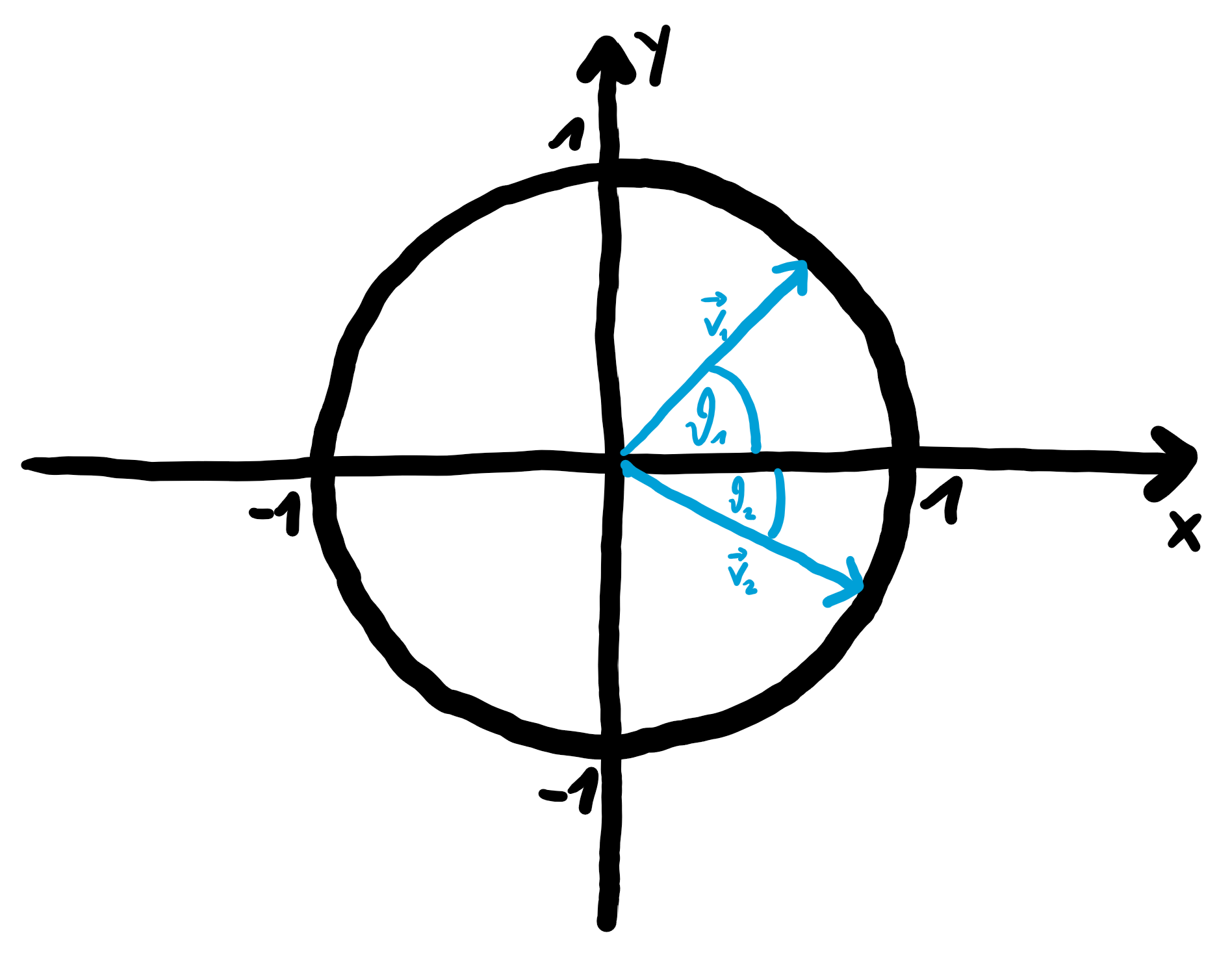
# Beweis
Sei $\theta$ der von den beiden Vektoren $\vec{v_1}$ und $\vec{v_2}$ eingeschlossene Winkel. Für das Skalarprodukt der beiden Vektoren gilt dann: $$\vec{v_1} \cdot \vec{v_2}=|\vec{v_1}||\vec{v_2}|\cos\theta$$
Da $\vec{v_1}$ und $\vec{v_2}$ Vektoren im Einheitskreis sind, gilt ferner: $|\vec{v_1}|=1$ und $|\vec{v_2}|=1$.
Da $\theta=\theta_{1}+\theta_{2}$ erhalten wir:
$$\vec{v_1} \cdot \vec{v_2}=\cos(\theta_{1}+\theta_{2}) $$
Da $\vec{v_1}$ und $\vec{v_2}$ auf dem Einheitskreis liegen, können ihre Koordinaten mithilfe der trigonometrischen Funktionen beschrieben werden:
$$\vec{v_1}=\begin{pmatrix}\cos\theta_{1}\\ \sin\theta_{1}\end{pmatrix}; \quad \vec{v_2}=\begin{pmatrix}\cos\theta_{2}\\ -\sin\theta_2\end{pmatrix}$$
Einsetzen in obige Gleichung liefert:
$$\begin{pmatrix}\cos\theta_{1}\\ \sin\theta_{1}\end{pmatrix} \cdot \begin{pmatrix}\cos\theta_{2}\\ -\sin\theta_2\end{pmatrix}=\cos(\theta_{1}+\theta_{2})$$
Berechnen des Skalarprodukts gibt das gewünschte Resultat:
$$\cos\theta_{1}\cos\theta_{2}-\sin\theta_{1}\sin\theta_{2}=\cos(\theta_{1}+\theta_{2})$$