Anschauliche Erklärung Minus mal Minus ist Plus
Die folgende anschauliche Erklärung, warum die Multiplikation zweier negativer Zahlen eine positive Zahl ergibt, habe ich im Rahmen des Make Math Moments Virtual Summit 2022 in einem Vortrag von James Tanton gehört.
Sie ist keine saubere mathematische Erklärung, bietet aber eine gute intuitive Erklärung, die gerade für Schüler zugänglicher ist, als die vollständige algebraische Erklärung.
# Plus mal Minus & Minus mal Plus
Vorausgesetzt wird, dass man akzeptiert, dass eine positive Zahl multipliziert mit einer negativen Zahl wieder eine negative Zahl ergibt. Dies ist im Kontext mit z. B. Schulden oder Höhenangaben den meisten Schülern klar. $5 \cdot (-4)=-20$ könnte z. B. heißen, dass ich $5$-mal $4$ Meter nach unten gehe, also bin ich insgesamt $20$ Meter nach unten gegangen.
$(-4) \cdot 5 = -20$ macht da schon weniger Sinn. $-4$-mal $5$ Meter zu gehen, ist schwer vorstellbar. Da man aber will, dass $a \cdot b = b \cdot a$ ist, kann man einfach sagen, dass $(-4) \cdot 5 = 5 \cdot (-4)$ ist und umgeht dieses Problem damit.
Bei dem Fall Minus mal Minus funktioniert das nicht mehr.
# Minus mal Minus
Im Folgenden wird das Produkt $17 \cdot 18$ auf vier verschiedene Arten berechnet.
Multiplikation kann man sich als Flächenberechnung eines Rechtecks vorstellen, in unserem Fall mit den Seitenlängen $17$ und $18$. Wir werden die Seitenlängen im Folgenden unterschiedlich aufteilen, jedoch wird sich der Flächeninhalt dadurch nicht verändern.
# 1. Möglichkeit
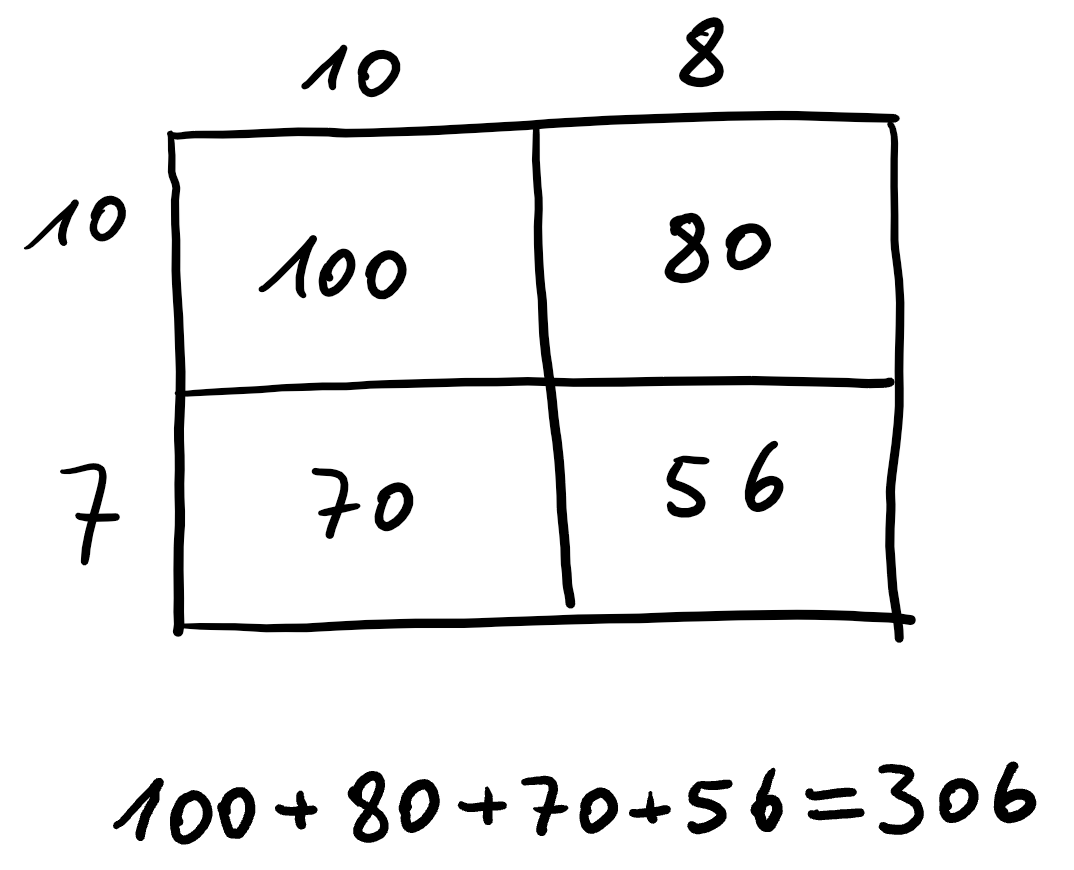
# 2. Möglichkeit
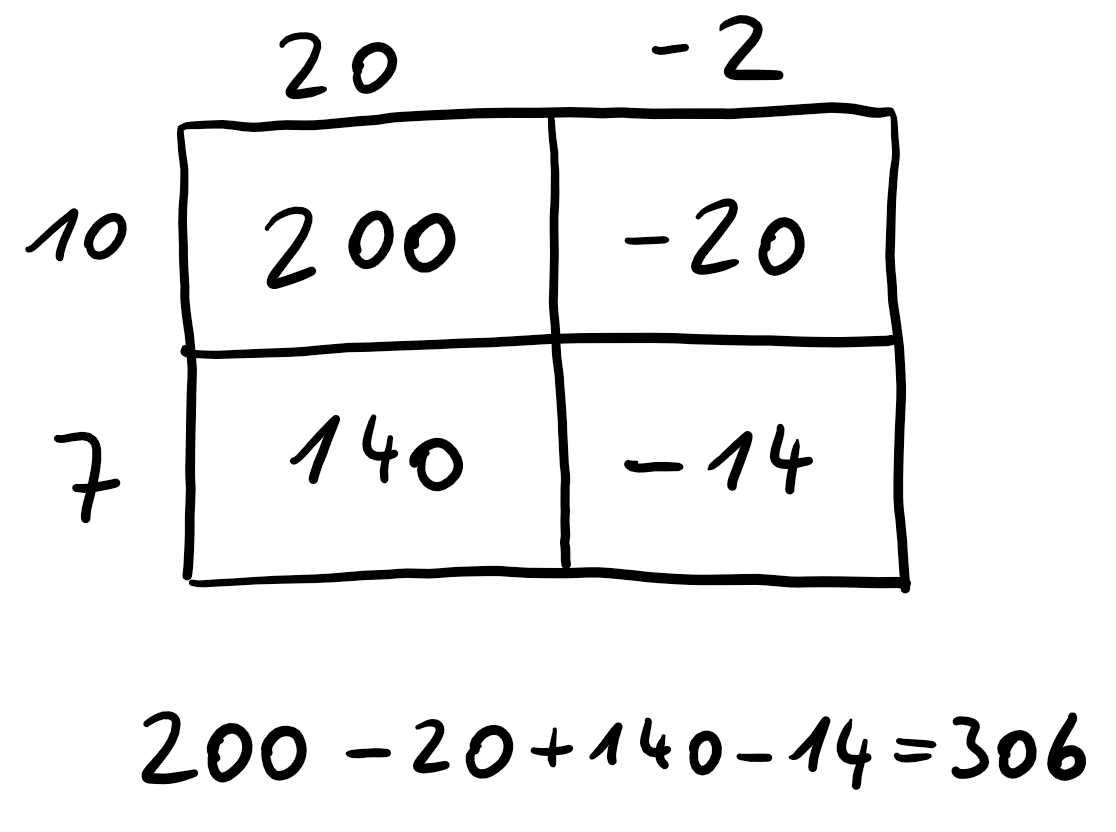
# 3. Möglichkeit
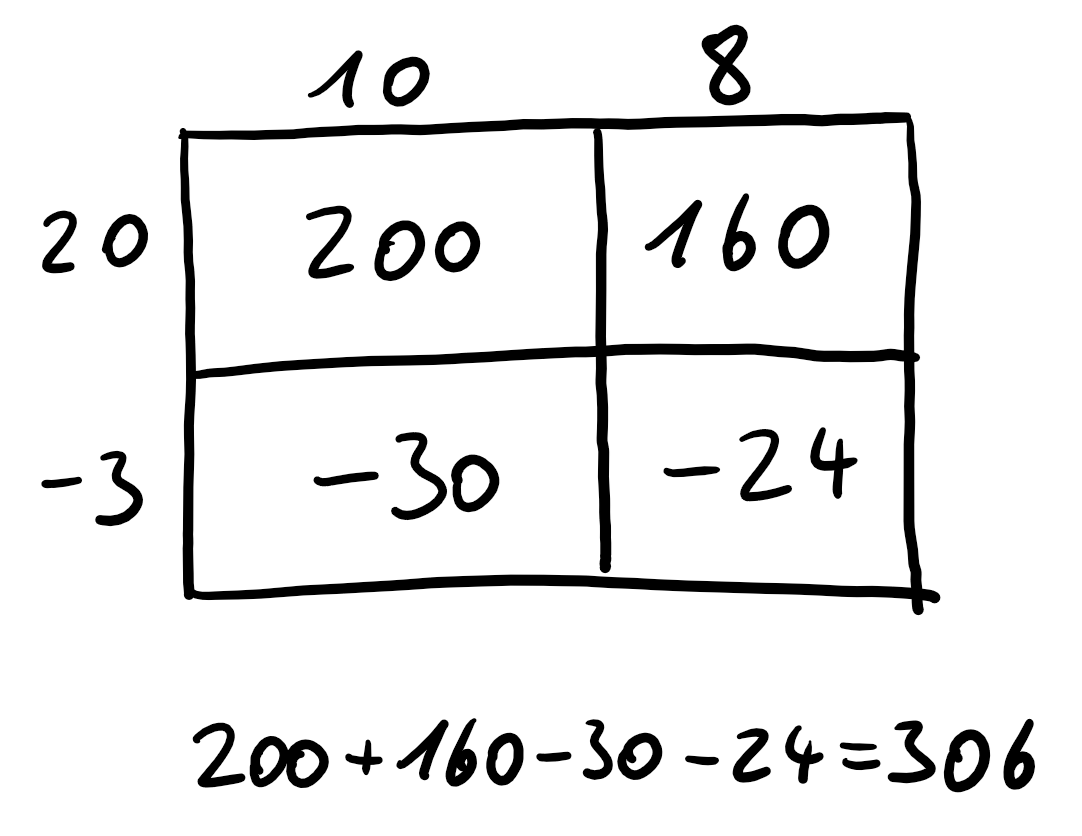
# 4. Möglichkeit
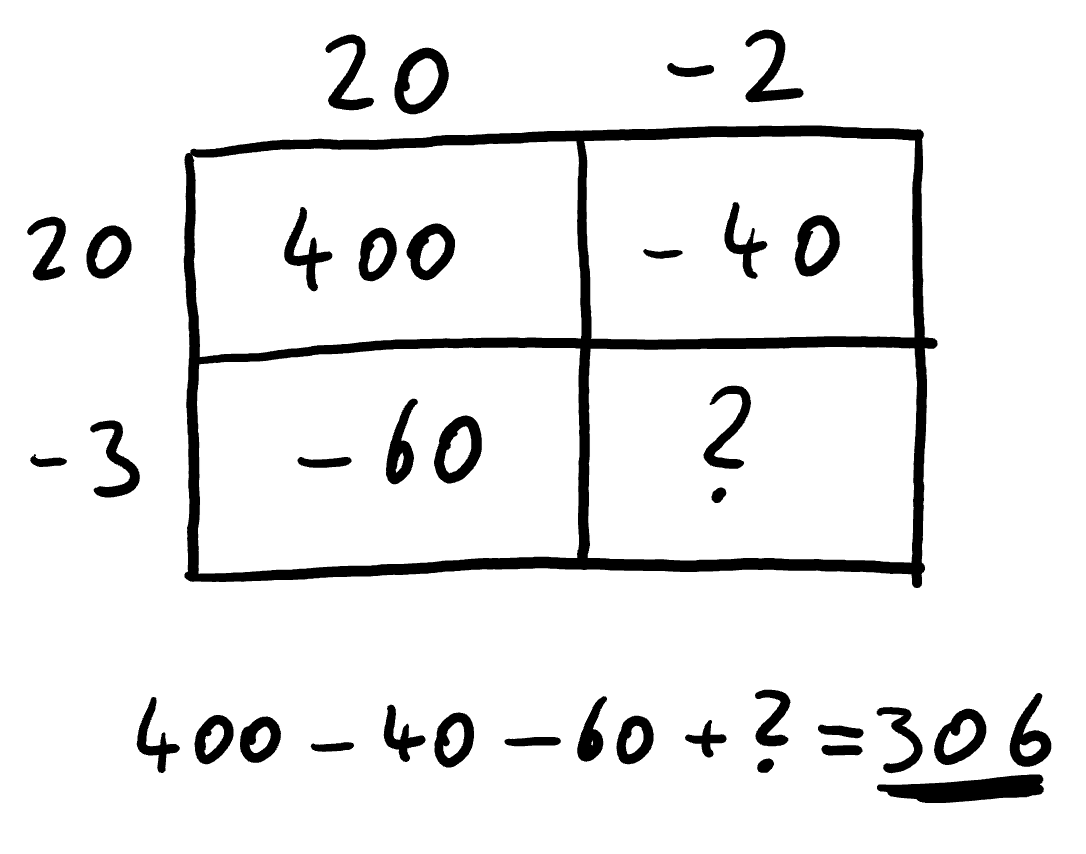
Da die Summe der Teilrechtecke wieder $306$ ergeben muss, muss das Rechteck mit dem $?$ den Flächeninhalt $6$ haben.
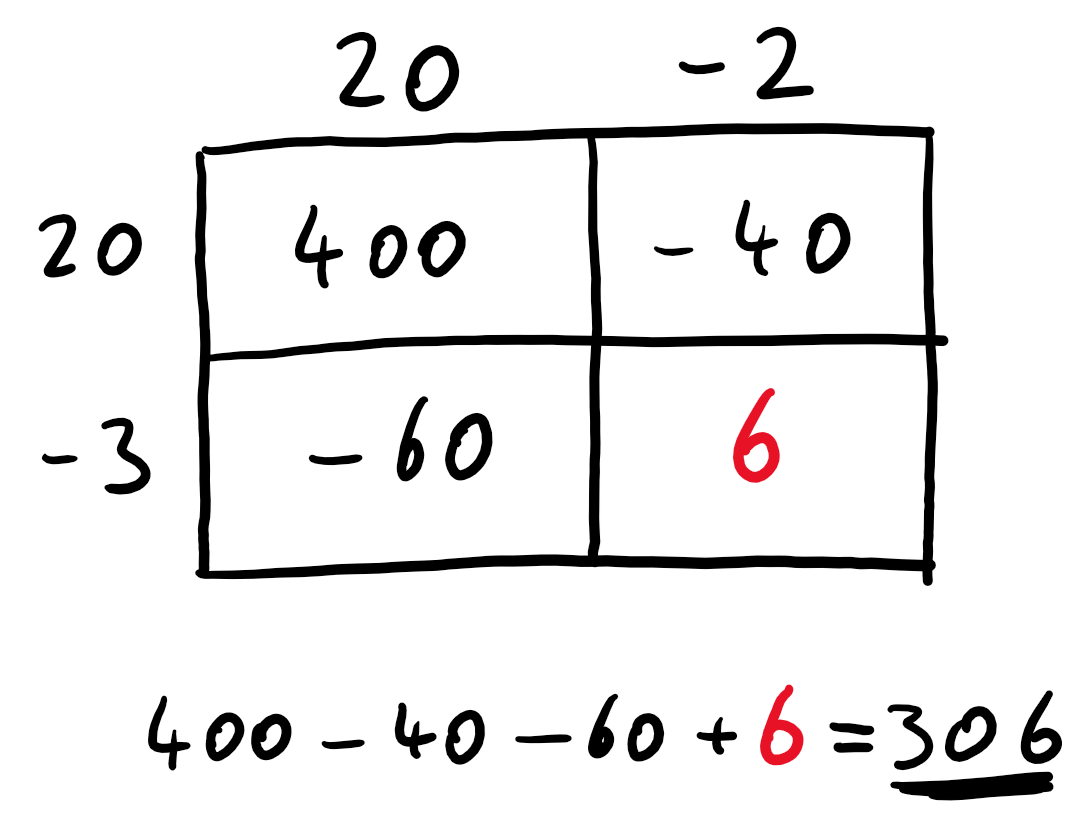
Es folgt also, dass $(-3) \cdot (-2) = 6$.
# Aufgabe für Schüler
Überzeuge mich, dass $(-4)\cdot (-5)=20$ ist. Fange hierfür vielleicht mit $16 \cdot 15$ an.