Beliebige Münzen simulieren
# Faire Münze mit gezinkter Münze simulieren
Hat man nur eine gezinkte oder eine möglicherweise gezinkte Münze zur Hand, kann man mit dieser trotzdem einen fairen Münzwurf simulieren.
Nehmen wir beispielhaft an, dass unsere Münze zu 70 % auf Kopf landet. Die folgende Argumentation lässt sich jedoch genauso gut mit jeder anderen Wahrscheinlichkeit führen.
Werfen wir die Münze zweimal so erhalten wir die folgende Wahrscheinlichkeitesverteilung:
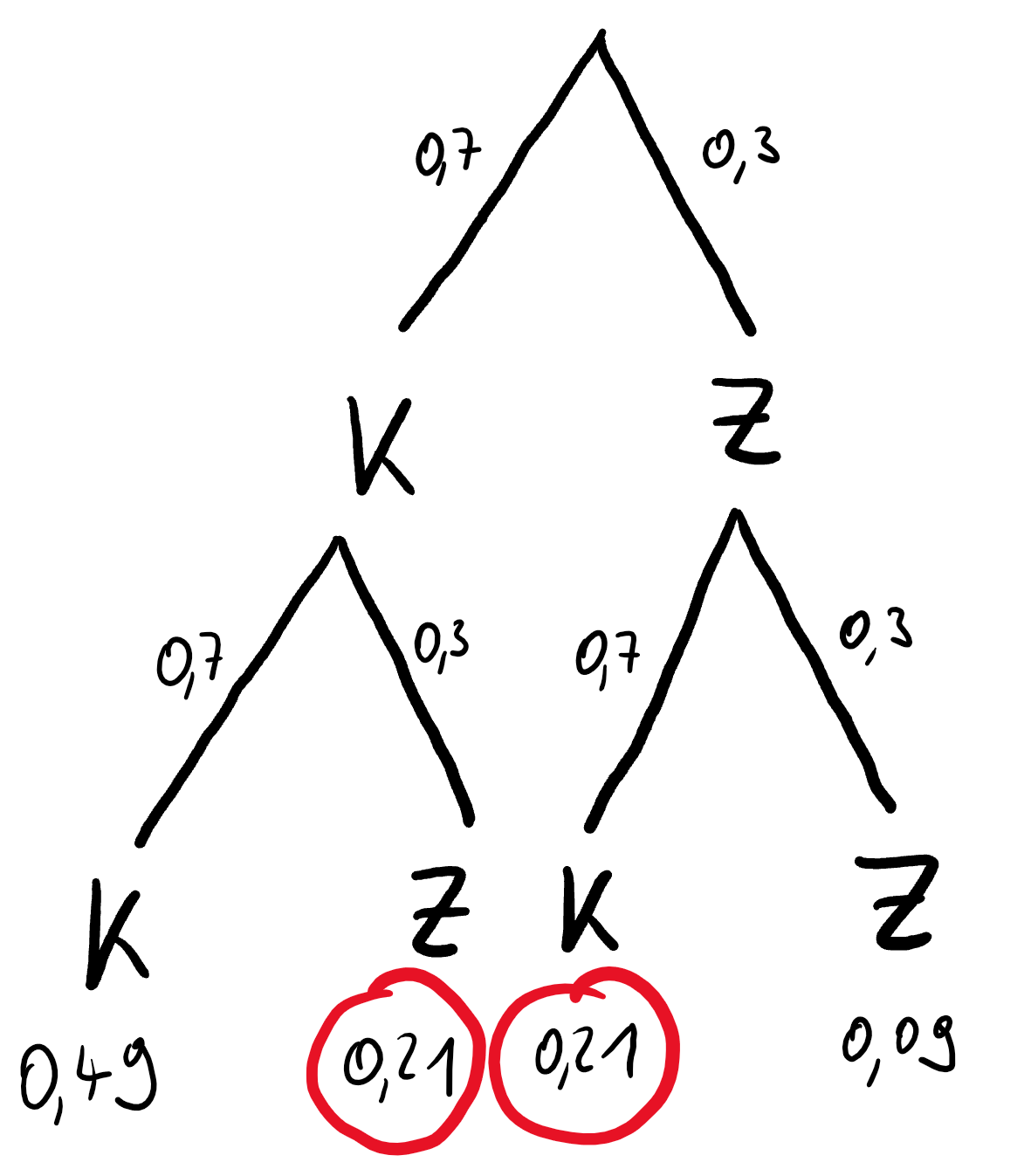
Die Wahrscheinlichkeit für $Kopf, Zahl$ ist somit genauso groß, wie für $Zahl, Kopf$. Wir haben also zwei Ereignisse, die gleich wahrscheinlich sind, genau wie bei einem fairen Münzwurf.
Sollte zweimal dasselbe geworfen werden, also $Kopf, Kopf$ oder $Zahl, Zahl$, so wirft man einfach erneut.
Im weiteren Verlauf wird die Seite $Kopf$ mit der Zahl $0$ identifiziert und die Seite $Zahl$ mit der Zahl $1$.
# Diagramm
ist das Ergebnis])
# Beliebige Münze mit fairer Münze simulieren
Andersherum lässt sich mithilfe einer fairen Münze auch eine gezinkte Münze simulieren. Die Wahrscheinlichkeit für $Kopf$ können wir dabei beliebig wählen.
Wir wollen beispielhaft eine Münze, die mit einer Wahrscheinlichkeit von $\frac{2}{7}$ $Kopf$ zeigt, simulieren.
Der Trick besteht darin, die gewünschte Wahrscheinlichkeit im Binärsystem zu schreiben: $$\frac{2}{7}=0,0100100100100\ldots_{2}$$
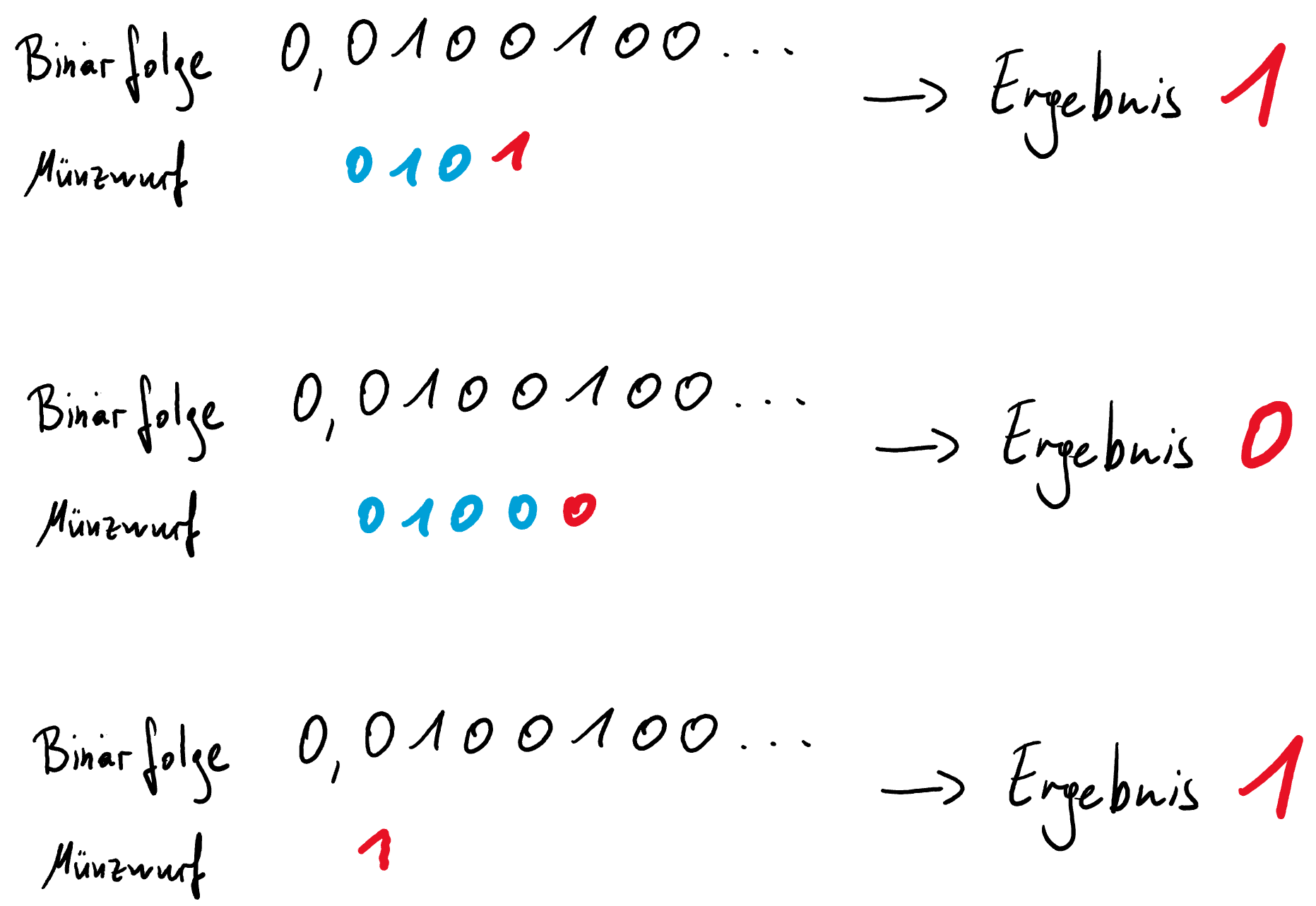
Nun wirft man die faire Münze und vergleicht das Ergebnis des 1. Wurfs mit der 1. Nachkommastelle der Binärfolge.
Ist sie gleich, so geht man zur nächsten Nachkommastelle und vergleicht diese mit dem Ergebnis des folgenden Münzwurfs.
Dies wiederholt man solange bis sich Nachkommastelle und Münzwurf unterscheiden. Das Ergebnis dieses Münzwurfs ist dann das Ergebnis des simulierten gezinkten Münzwurfs.
In unserem Beispiel erhält man so das Ergebnis $0$ (also $Kopf$) mit einer Wahrscheinlichkeit von $\frac{2}{7}$.
# Diagramm
Binärfolge markieren]) --> B[Münze werfen] B --> C[Geworfene und
markierte Ziffer
vergleichen
] C -->|Stimmen
überein| D[Folgende
Nachkomma-
stelle markieren
] D --> B C -->|Stimmen
nicht überein| E([Geworfene Ziffer
ist das Ergebnis])
# Beispiele
# Erklärung
Um Verwirrungen vorzubeugen, werden im folgenden Abschnitt die Ergebnisse der fairen Münze in blau und die Ergebnisse der simulierten gezinkten Münze in rot geschrieben.
Schauen wir uns zunächst noch einmal die Binärfolge von oben an und machen uns klar, was die einzelnen Nachkommastellen bedeuten:
$$\begin{align*} \frac{2}{7}&=0,0100100100100\ldots_{2}\\ &=0\cdot\left(\frac{1}{2}\right)^{1}+1\cdot\left(\frac{1}{2}\right)^{2}+0\cdot\left(\frac{1}{2}\right)^{3}+0\cdot\left(\frac{1}{2}\right)^{4}+1\cdot\left(\frac{1}{2}\right)^{5}+\\ &\phantom{=~}0\cdot\left(\frac{1}{2}\right)^{6}+0\cdot\left(\frac{1}{2}\right)^{7}+1\cdot\left(\frac{1}{2}\right)^{8}+0\cdot\left(\frac{1}{2}\right)^{9}+0\cdot\left(\frac{1}{2}\right)^{10}\ldots\\ &=1\cdot\left(\frac{1}{2}\right)^{2}+1\cdot\left(\frac{1}{2}\right)^{5}+1\cdot\left(\frac{1}{2}\right)^{8}+1\cdot\left(\frac{1}{2}\right)^{11}+\ldots\\ &=\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{5}+\left(\frac{1}{2}\right)^{8}+\left(\frac{1}{2}\right)^{11}+\ldots \end{align*} $$
Wir wollen nun zeigen, dass dies auch genau die Wahrscheinlichkeit ist, mit der gezinkten Münze eine $\textcolor{red}{0}$ zu werfen.
Mit dem oben genannten Verfahren können wir mit der simulierten gezinkten Münze nur eine $\textcolor{red}{0}$ bekommen, wenn die Binärfolge eine $1$ zeigt. Dies ist nur beim 2. Wurf, 5. Wurf. 8. Wurf, 11. Wurf etc. der Fall.
Wollen wir im 2. Wurf eine $\textcolor{cyan}{0}$ werfen, so muss auch der Wurf davor mit der Binärfolge übereinstimmen. Die Wahrscheinlichkeit hierfür ist $\left(\frac{1}{2}\right)^{2}$.
Wir könnten auch im 5. Wurf eine $\textcolor{cyan}{0}$ werfen. Auch hier müssen alle vorherigen Würfe mit der Binärfolge übereinstimmen. Die Wahrscheinlichkeit für eine $\textcolor{cyan}{0}$ im 5. Wurf beträgt also $\left(\frac{1}{2}\right)^{5}$.
Die Wahrscheinlichkeit für eine $\textcolor{cyan}{0}$ im 8. Wurf beträgt $\left(\frac{1}{2}\right)^{8}$ usw.
Die Wahrscheinlichkeit für eine $\textcolor{red}{0}$ beträgt also wie gewollt:
$$\begin{align*} P(\textcolor{red}{0})&=P(\textcolor{cyan}{0}\text{ im 2. Wurf}) + P(\textcolor{cyan}{0}\text{ im 5. Wurf}) + P(\textcolor{cyan}{0}\text{ im 8. Wurf}) + \ldots\\ &=\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{5}+\left(\frac{1}{2}\right)^{8}+\left(\frac{1}{2}\right)^{11}+\ldots\\ &=\frac{2}{7} \end{align*}$$
Quelle: https://jeremykun.com/2014/02/12/simulating-a-biased-coin-with-a-fair-coin/
# Beliebige Münze mit beliebiger Münze simulieren
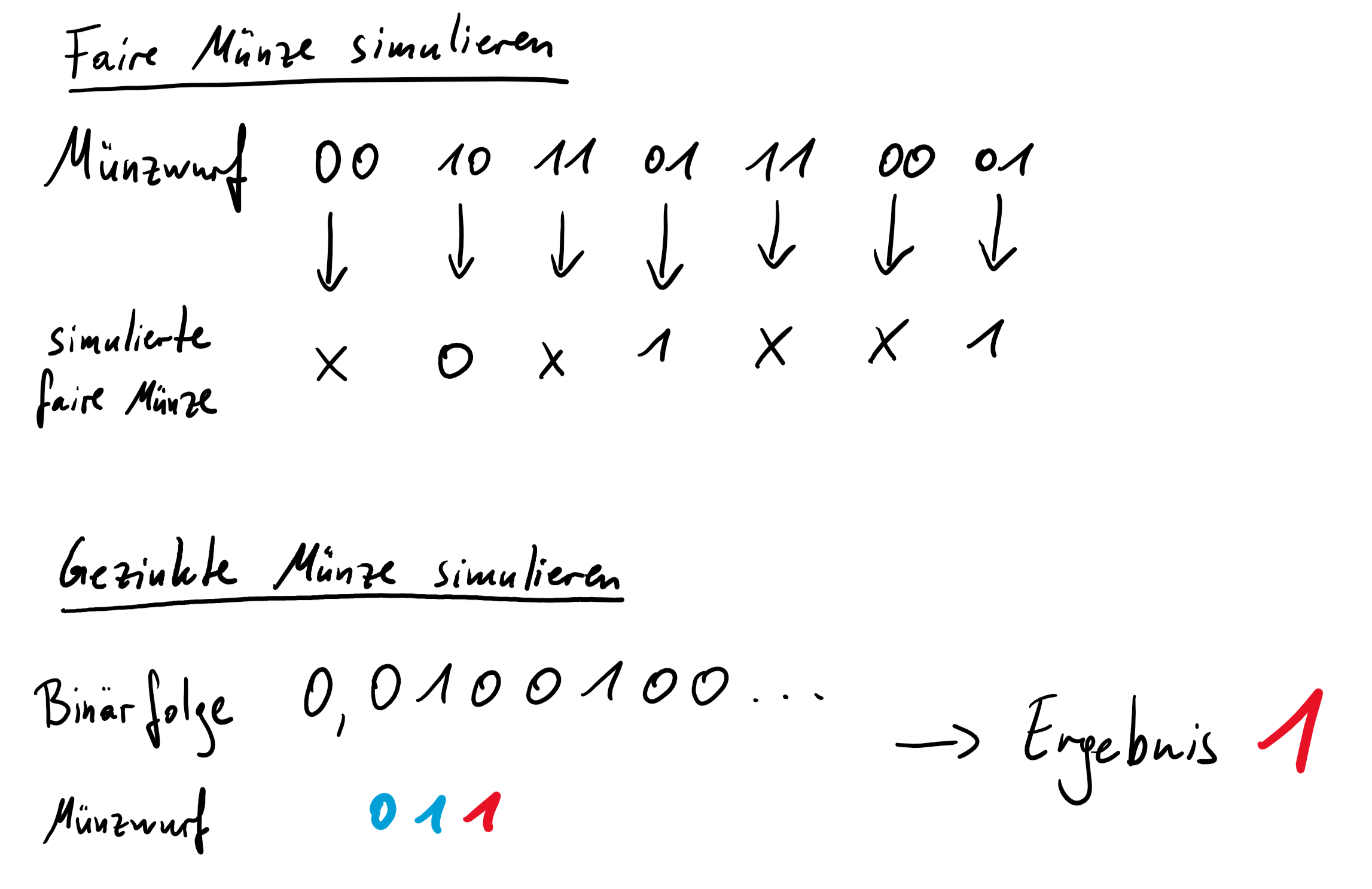
Bringen wir beide Verfahren zusammen so können wir mit einer gezinkten Münze zunächst eine faire Münze simulieren, um mit dieser anschließend eine beliebige Münze zu simulieren.
Wir können also mit jeder beliebigen Münze jede andere beliebige Münze simulieren.1
# Diagramm
Binärfolge markieren]) --> V[Münze zweimal werfen] V --> W[00 oder 11?] W -->|ja| V W -->|nein| X[Zuletzt geworfene
und markierte
Ziffer vergleichen
] X -->|Stimmen
überein| D[Folgende
Nachkomma-
stelle markieren
] D --> V X -->|Stimmen
nicht überein| E([Zuletzt geworfene
Ziffer ist das Ergebnis])
# Beispiel
Sofern die Münze nicht zu 100 % auf einer Seite landet. ↩︎