Beweis Hauptsatz der Differential- und Integralrechnung für ganzrationale Funktionen
# Definition Integral
Sei $f$ eine stetige Funktion für alle $x\in[a,~b]$. Seien $U_{n}$ und $O_{n}$ die Unter- bzw. Obersummen mit $n$ Teilintervallen auf $[a,~b]$. Dann definieren wir das Integral von $f$ auf dem Intervall $[a,~b]$ wie folgt:
$$\lim_{n\to\infty} U_{n} = \lim_{n\to\infty} O_{n} = \int_{a}^{b} f(x)~\mathrm{d}x$$
# Satz
Sei $f$ eine stetige ganzrationale1 Funktion für alle $x\in[a,b]$. Sei $F$ die Funktion, die einer Stelle $x_{0}$ die Fläche unter dem Graphen $f$ im Intervall $[0,x_{0}]$ zuordnet.
Dann gilt für alle $x\in[a,b]$:
$$F’(x)=f(x).$$
Ferner gilt:
$$\int_{a}^{b} f(x)~\mathrm{d}x=F(b)-F(a).$$
# Beweis
Die Funktion $F$ gibt uns die Fläche unter dem Graphen $f$; es ist jedoch noch nicht klar, dass diese Funktion $F$ auch tatsächlich die Stammfunktion von $f$ ist. Dies werden wir im Folgenden zeigen.
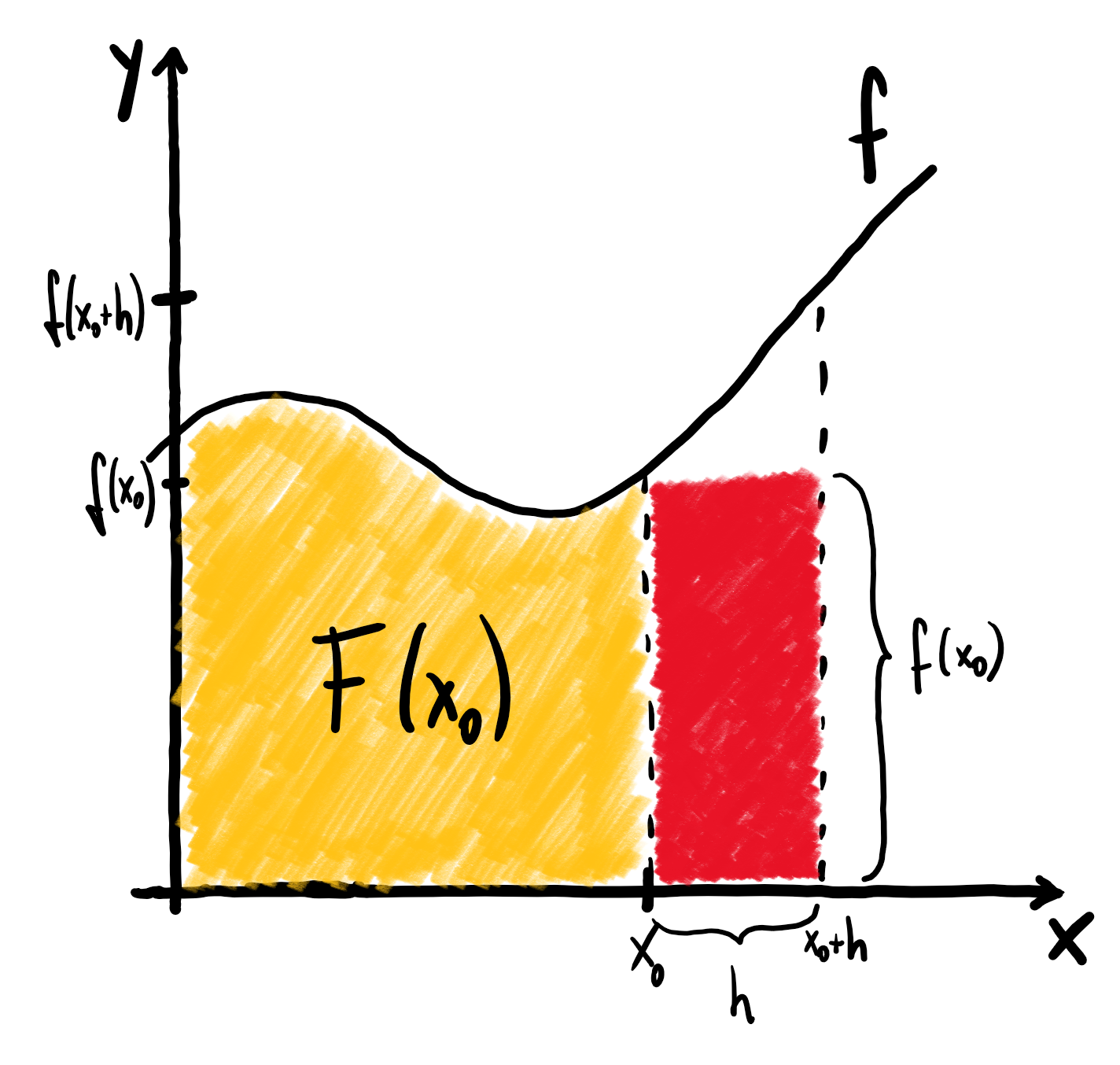
Sei $x_{0}\in[a,b]$ beliebig. Schauen wir uns die Fläche unter dem Graphen von $f$ im Intervall $[x_{0},x_{0}+h]$ mit $h>0$ an. Der Flächeninhalt dieses Stücks ist per Definition gegeben durch $F(x_{0}+h)-F(x_{0})$. Das gesuchte Flächenstück ist in der untenstehenden Abbildung in rot eingezeichnet.
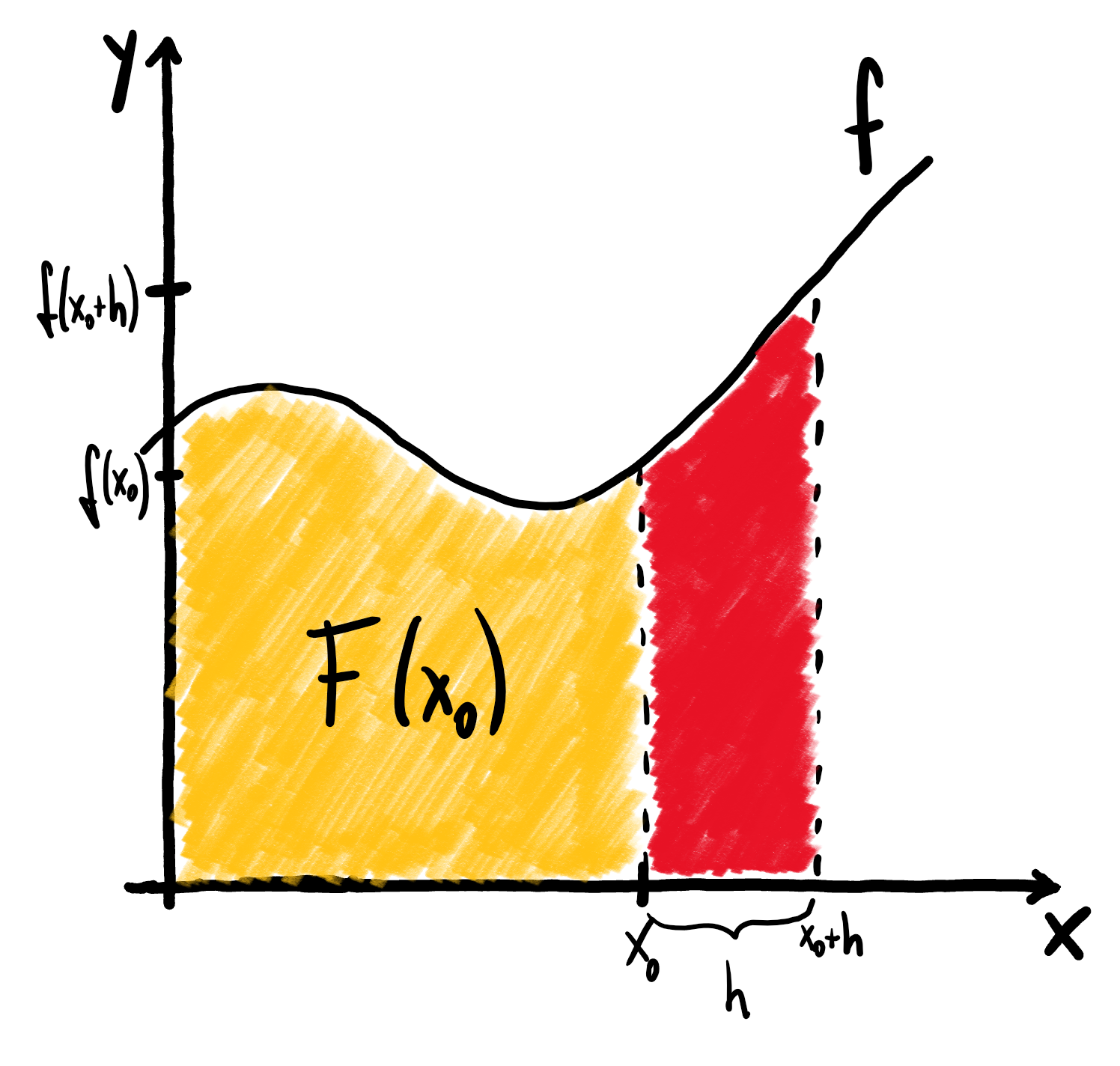
Nach der Definition des Integrals und von $F$ gilt also für den gesuchten Flächeninhalt:
$$ \begin{align*} \int\limits_{x_{0}}^{x_{0}+h} f(x)~\mathrm{d}x &= \int\limits_{0}^{x_{0}+h} f(x)~\mathrm{d}x - \int\limits_{0}^{x_{0}} f(x)~\mathrm{d}x\\\ &= F(x_{0}+h)-F(x_{0}). \end{align*} $$
Wir können erkennen, dass wenn wir $h$ nur genügend klein wählen, die ganzrationale Funktion $f$ im Intervall $[x_{0},x_{0}+h]$ entweder monoton steigend oder monoton fallend ist.
Im Folgenden gehen wir davon aus, dass $f$ im Intervall $[x_{0},x_{0}+h]$ monoton steigend ist. Der Beweis für den Fall monoton fallend verläuft analog, ist aber dem Leser als Aufgabe überlassen.
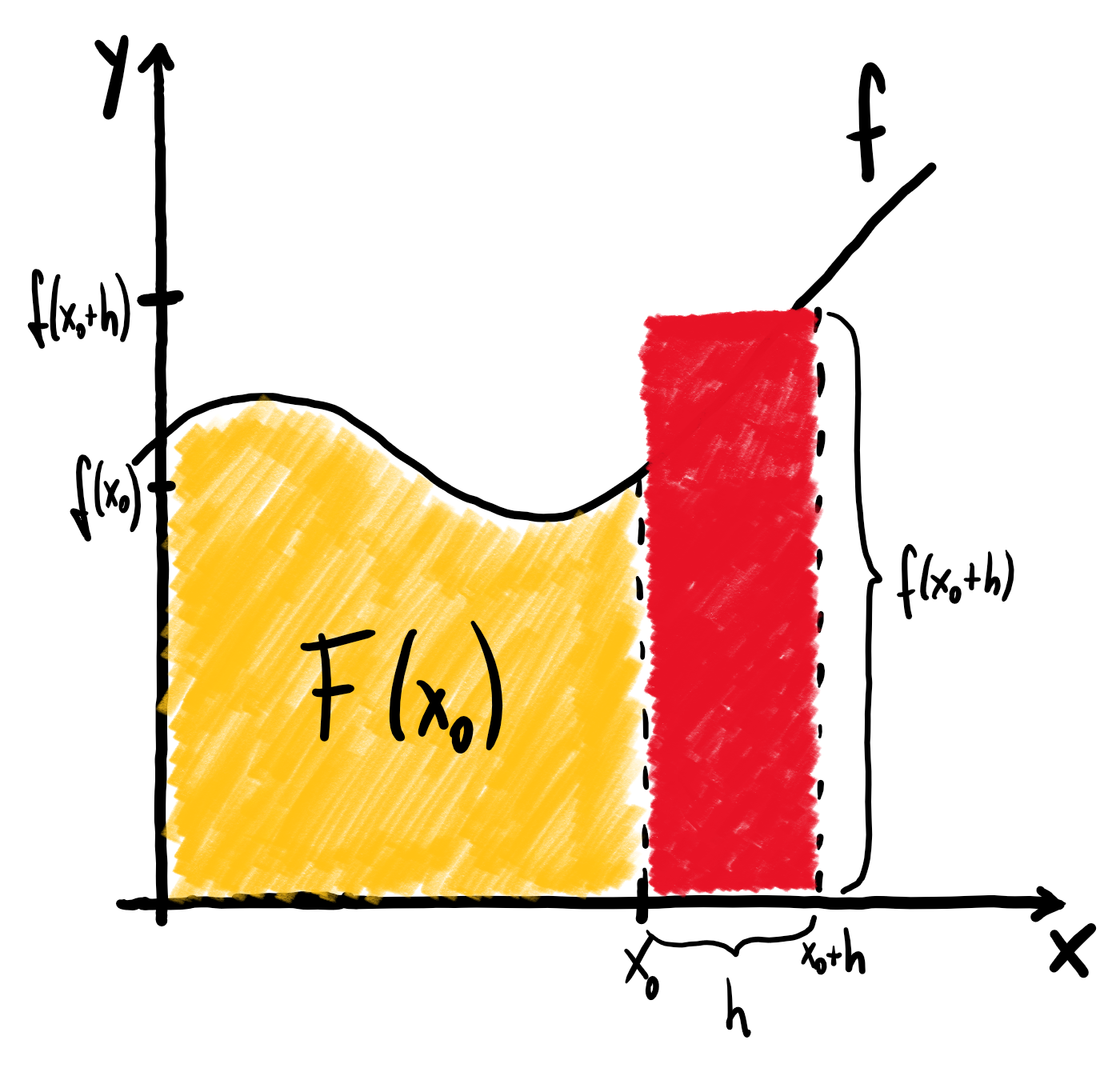
Wir schätzen nun ähnlich wie bei der Unter- und Obersumme die Fläche unter dem Graphen von $f$ im Intervall $[x_{0},x_{0}+h]$ nach unten und nach oben ab:
Es ergibt sich:
Antwort
$$f(x_{0}) \cdot h \leq F(x_{0}+h)-F(x_{0}) \leq f(x_{0}+h) \cdot h$$
Da $h>0$ folgt nach Division durch $h$:
Antwort
$$f(x_{0}) \leq \frac{F(x_{0}+h)-F(x_{0})}{h} \leq f(x_{0}+h)$$
Für $h \to 0$ gilt:
Antwort
$$f(x_{0}) \leq F’(x_{0}) \leq f(x_{0}).$$
Aufgabe
Begründen Sie, warum für $h\to 0$ gilt: $f(x_{0}+h)=f(x_{0}).$
Begründen Sie, warum für $h\to 0$ gilt: $\frac{F(x_{0}+h)-F(x_{0})}{h} = F’(x_{0}).$
Es gilt also wie gewollt:
$$F’(x_{0})=f(x_{0}).$$
Aufgabe
Führen Sie das fehlende Beweisstück für den Fall, dass $f$ auf dem Intervall $[x_{0},x_{0}+h]$ monoton fallend ist.
Wir wissen nun also, dass die Stammfunktion von $f$ tatsächlich die Funktion ist, die uns die Fläche unter dem Graphen von $f$ liefert.
Sei $F$ eine Stammfunktion von $f$. Wir wissen, dass das Addieren einer Konstante $C$ zu einer Stammfunktion uns eine weitere Stammfunktion liefert. Es gilt also für eine beliebige andere Stammfunktion $G$ von $f$, dass $F(x)=G(x)+C$ mit $C\in \mathbb{R}$.
Es bleibt noch zu zeigen, dass für jede beliebige Stammfunktion $G$ von $f$ gilt:
$$\int_{a}^{b} f(x)~\mathrm{d}x=G(b)-G(a).$$
Es gelte für eine bekannte Stammfunktion $F$ von $f$:
$$\int_{a}^{b} f(x)~\mathrm{d}x=F(b)-F(a).$$
Für eine beliebige Stammfunktion $G$ bedeutet das:
Antwort
$$\begin{align*} \int_{a}^{b} f(x)~\mathrm{d}x&=F(b)-F(a)\\ &=\left(G(b)+C\right)-\left(G(a)+C\right)\\ &=G(b)-G(a) \end{align*}$$
Die Konstante $C$ fällt also nach der Subtraktion weg.
Der Hauptsatz der Differential- und Integralrechnung gilt also für alle Stammfunktionen von $f$.
Der Beweis für beliebige stetige Funktionen wird meist mithilfe des Mittelwertsatzes der Integralrechnung geführt. ↩︎