Die zwei Darstellungsarten des Skalarprodukts

Zuletzt aktualisiert Apr 8, 2023 Quelldatei anzeigen

HINWEIS: Bitte die Seite ein zweites Mal laden. Die Animationen laden momentan leider noch nicht, wie sie sollen.

Betrachten wir zwei Vektoren $\vec{a}$ und $\vec{b}$ aus dem $\mathbb{R}^{n}$, welche einen Winkel von $\theta$ einschließen. Das Skalarprodukt dieser beiden Vektoren lässt sich auf zwei verschiedene Arten darstellen und berechnen:

$$\begin{aligned} &1. \quad \vec{a}\cdot\vec{b} = a_{1}b_{1}+a_{2}b_{2}+\ldots+a_{n}b_{n} = \sum\limits_{i=1}^{n}{a_{i}b_{i}} \\ &2. \quad \vec{a}\cdot\vec{b} = \lVert\vec{a}\rVert \, \lVert\vec{b}\rVert \cos\theta \end{aligned}$$

In der ersten Variante werden die entsprechenden Einträge der beiden Vektoren multipliziert und die Ergebnisse schließlich addiert. Die zweite Variante lässt sich sehr schön grafisch interpretieren. Projiziert man den Vektor $\vec{b}$ auf den Vektor $\vec{a}$, so entspricht das Skalarprodukt dem Produkt aus der Länge von $\vec{a}$ und der Länge der Projektion von $\vec{b}$.

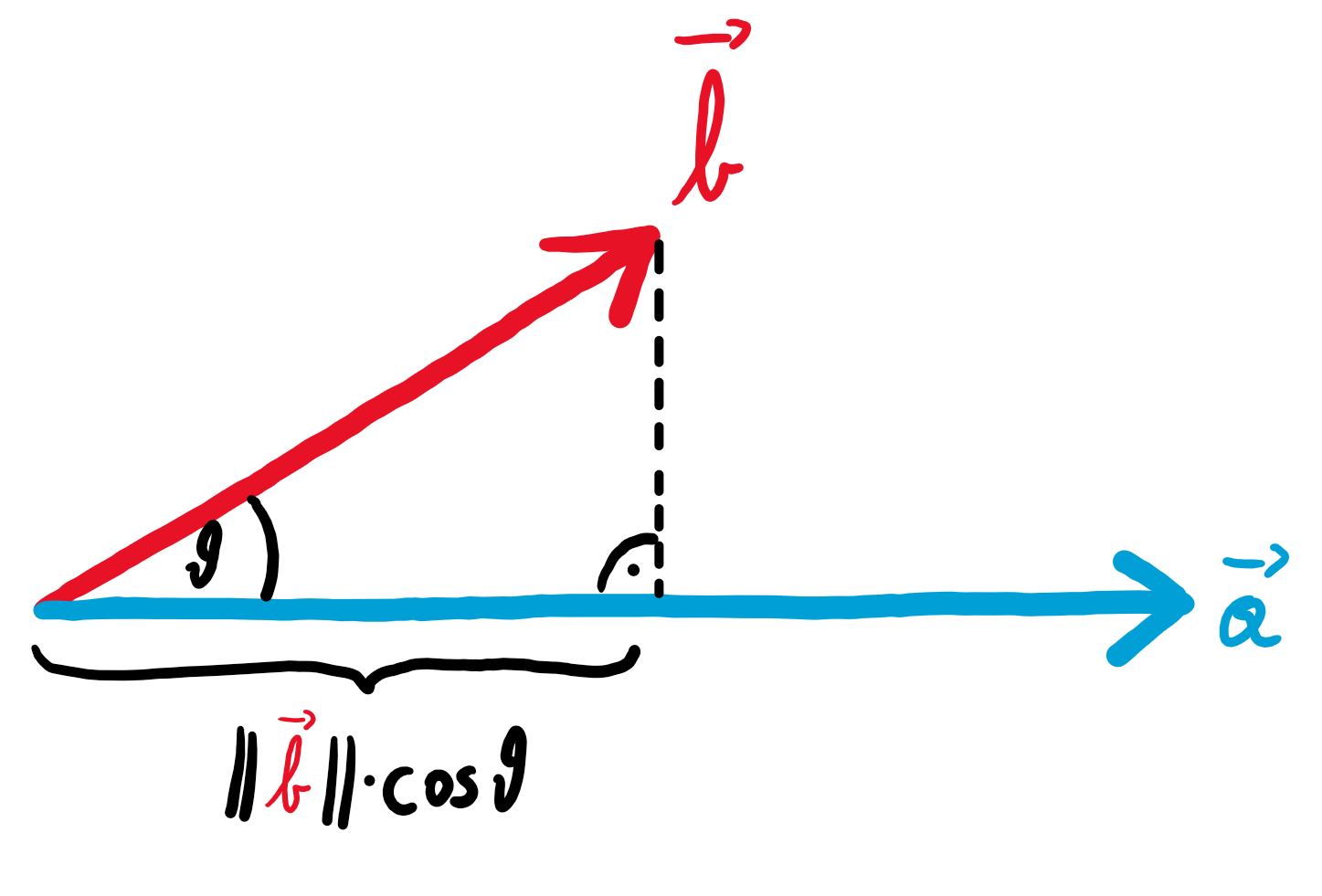
Die erste Variante bietet vor allem eine sehr einfache Berechnung des Skalarprodukts, wohingegen die zweite rechnerisch komplizierter ist, jedoch die Bestimmung des Winkels $\theta$ ermöglicht. Warum das Skalarprodukt so definiert ist, wird an dieser Stelle kurz erklärt.

Doch warum sind diese scheinbar so unterschiedlichen Darstellungsarten äquivalent?

Wir zeigen nun mit rein algebraischen Mitteln, dass beide Darstellungen des Skalarprodukts äquivalent sind.

Interpretieren wir die beiden Vektoren $\vec{a}$ und $\vec{b}$ als zwei Seiten eines Dreiecks, die den Winkel $\theta$ einschließen und den Vektor $\vec{b}-\vec{a}$ als dritte Seite.

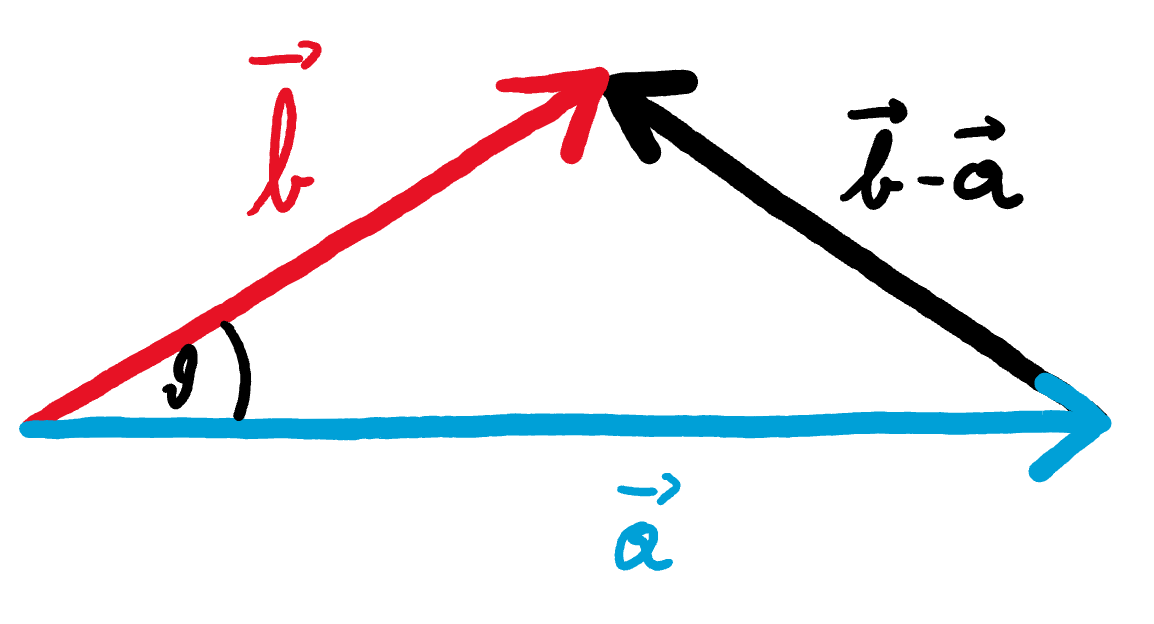
Nach dem Kosinussatz gilt:

$$\lVert \vec{b}-\vec{a} \rVert^{2} = \lVert \vec{a} \rVert^{2} + \lVert \vec{b} \rVert^{2} - 2 \, \lVert \vec{a} \rVert \, \lVert \vec{b} \rVert \cos\theta$$

Daraus folgt:

$$\begin{aligned} 2 \, \lVert \vec{a} \rVert \, \lVert \vec{b} \rVert \cos\theta &= \lVert \vec{a} \rVert^{2} + \lVert \vec{b} \rVert^{2} - \lVert \vec{b}-\vec{a} \rVert^{2} \\\ &= \sum\limits_{i=1}^{n}{a_{i}^{2}}+\sum\limits_{i=1}^{n}{b_{i}^{2}}-\sum\limits_{i=1}^{n}{(b_{i}-a_{i})^{2}} \\\ &= \sum\limits_{i=1}^{n}{a_{i}^{2}}+\sum\limits_{i=1}^{n}{b_{i}^{2}}- \sum\limits_{i=1}^{n}{\left(b_{i}^{2}-2a_{i}b_{i}+a_{i}^{2}\right)}\\\ &= \sum\limits_{i=1}^{n}{a_{i}^{2}}+\sum\limits_{i=1}^{n}{b_{i}^{2}}- \sum\limits_{i=1}^{n}{b_{i}^{2}} + 2 \cdot \sum\limits_{i=1}^{n}{a_{i}b_{i}} - \sum\limits_{i=1}^{n}{a_{i}^{2}}\\\ &=2 \cdot \sum\limits_{i=1}^{n}{a_{i}b_{i}} \end{aligned}$$

Dividiert man beide Seiten durch $2$ ergibt sich die gewünschte Gleichheit:

$$\lVert \vec{a} \rVert \, \lVert \vec{b} \rVert \cos\theta = \sum\limits_{i=1}^{n}{a_{i}b_{i}}$$

Dieser Beweis zeigt zwar rechnerisch sehr prägnant, warum die beiden Darstellungsarten des Skalarprodukts äquivalent sind, jedoch haben wir dadurch kein wirkliches Verständnis dafür gewonnen, warum dies so ist.

Im Folgenden werden wir zeigen, dass man das Skalarprodukt als lineare Abbildung betrachten kann, welche rechnerisch äquivalent zum Skalarprodukt ist. Anschließend werden wir nachweisen, dass diese Abbildung geometrisch gesehen genau die Eigenschaften hat, die auch das Skalarprodukt hat: Projektion und Streckung um Faktor der Länge des Vektors.

Machen wir hierfür zunächst einen Crashkurs zum Thema lineare Abbildungen.

Lineare Abbildungen sind Abbildungen zwischen zwei Vektorräumen, die bestimmte Eigenschaften erfüllen. An dieser Stelle reicht uns jedoch folgende Anschauung:

Der Nullpunkt bleibt fix und parallele Geraden, die jeweils den gleichen Abstand zueinander haben, bleiben nach der linearen Abbildung weiterhin parallel und haben weiterhin den gleichen Abstand zueinander.

Die folgende Animation zeigt dies beispielhaft:

Lineare Abbildungen lassen sich auf sehr einfache und elegante Weise mithilfe von Matrizen beschreiben. Durch die einschränkenden Bedingungen einer linearen Abbildung (fixer Nullpunkt, gleichbleibende Parallelität und gleichbleibender Abstand zwischen Geraden) sind nur wenige Eigenschaften nötig, um die Abbildung eindeutig zu beschreiben.

Es genügt bereits sich anzusehen, auf welche Vektoren die Einheitsvektoren $\vec{e}_{1} = \begin{pmatrix}\textcolor{red}{1}\\\textcolor{red}{0}\end{pmatrix}$ und $\vec{e}_{2}=\begin{pmatrix} \textcolor{turquoise}{0} \\ \textcolor{turquoise}{1} \end{pmatrix}$ abgebildet werden.

Schauen wir uns die oben gezeigte Abbildung erneut an, sehen wir, dass $\vec{e}_{1}$ auf den Vektor $\begin{pmatrix} \textcolor{red}{3} \\ \textcolor{red}{-1} \end{pmatrix}$ geschickt wird und der Vektor $\vec{e}_{2}$ auf den Vektor $\begin{pmatrix} \textcolor{turquoise}{-1} \\ \textcolor{turquoise}{2} \end{pmatrix}$.

Die gesamt lineare Abbildung lässt sich dann mithilfe der Matrix $\begin{pmatrix} \textcolor{red}{3} & \textcolor{turquoise}{-1} \\ \textcolor{red}{-1} & \textcolor{turquoise}{2} \end{pmatrix}$ beschreiben.

Was ist mit dem Vektor $\begin{pmatrix} 2 \\ 1 \end{pmatrix}$ eigentlich gemeint?

Anschaulich kann man sich darunter einen Pfeil vorstellen, der $2$ Einheiten in $x$-Richtung und $1$ Einheit in $y$-Richtung verläuft.

Da Vektoren jedoch im Allgemeinen nicht die Form von Pfeilen annehmen müssen, kann man einen Vektor allgemein als Linearkombination der jeweiligen Basisvektoren interpretieren. In unserem Falle:

$$\begin{pmatrix} 2 \\ 1 \end{pmatrix} = 2 \cdot \begin{pmatrix} \textcolor{red}{1} \\ \textcolor{red}{0} \end{pmatrix} + 1 \cdot \begin{pmatrix} \textcolor{turquoise}{0} \\ \textcolor{turquoise}{1} \end{pmatrix}$$

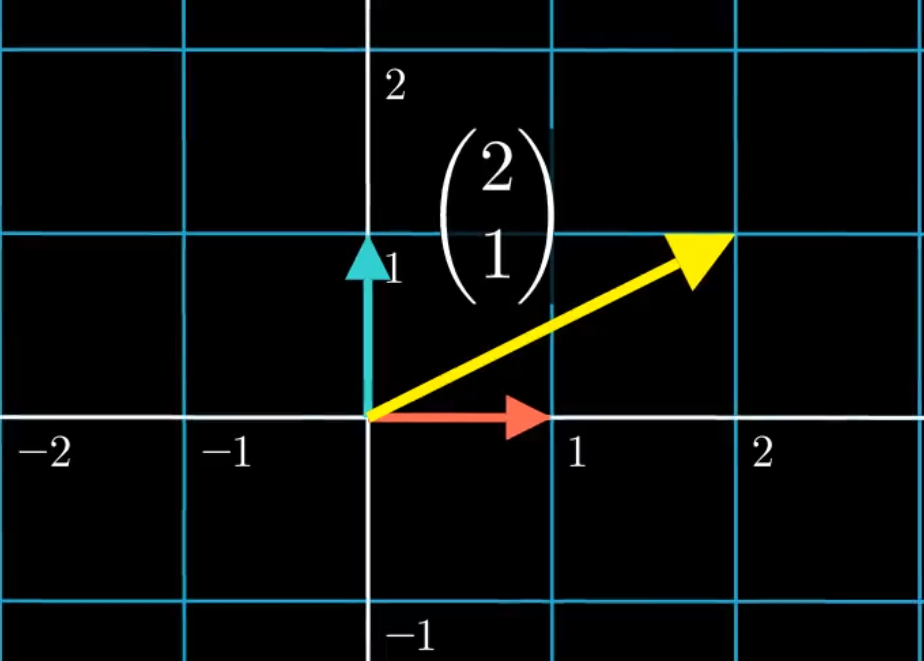
Der gesuchte Vektor ergibt sich also aus der Addition von zwei Kopien des ersten Basisvektors und einer Kopie des zweiten Basisvektors.

Diese Linearkombination kann man in verkürzter Form als Matrix-Vektor-Multiplikation ausdrücken:

$$2 \cdot \begin{pmatrix} \textcolor{red}{1} \\ \textcolor{red}{0} \end{pmatrix} + 1 \cdot \begin{pmatrix} \textcolor{turquoise}{0} \\ \textcolor{turquoise}{1} \end{pmatrix} = \begin{pmatrix} \textcolor{red}{1} & \textcolor{turquoise}{0} \\ \textcolor{red}{0} & \textcolor{turquoise}{1} \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix}$$

Diese Schreibweise bietet den Vorteil, dass man auf einfache Weise bestimmen kann, auf welchen Vektor eine lineare Abbildung einen beliebigen Vektor schickt.

Wollen wir z. B. herausfinden, was mit dem Vektor $\begin{pmatrix} 2 \\ 1 \end{pmatrix}$ nach der Anwendung der linearen Abbildung $\begin{pmatrix} 3 & -1 \\ -1 & 2 \end{pmatrix}$ passiert, so müssen wir nur die entsprechende Matrix austauschen.

$$\begin{pmatrix} \textcolor{red}{3} & \textcolor{turquoise}{-1} \\ \textcolor{red}{-1} & \textcolor{turquoise}{2} \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix} = 2 \cdot \begin{pmatrix} \textcolor{red}{3} \\ \textcolor{red}{-1} \end{pmatrix} + 1 \cdot \begin{pmatrix} \textcolor{turquoise}{-1} \\ \textcolor{turquoise}{2} \end{pmatrix} = \begin{pmatrix} 5 \\ 0 \end{pmatrix}$$

Durch die lineare Abbildung wird der Vektor $\begin{pmatrix} 2 \\ 1 \end{pmatrix}$ also auf den Vektor $\begin{pmatrix} 5 \\ 0 \end{pmatrix}$ geschickt.

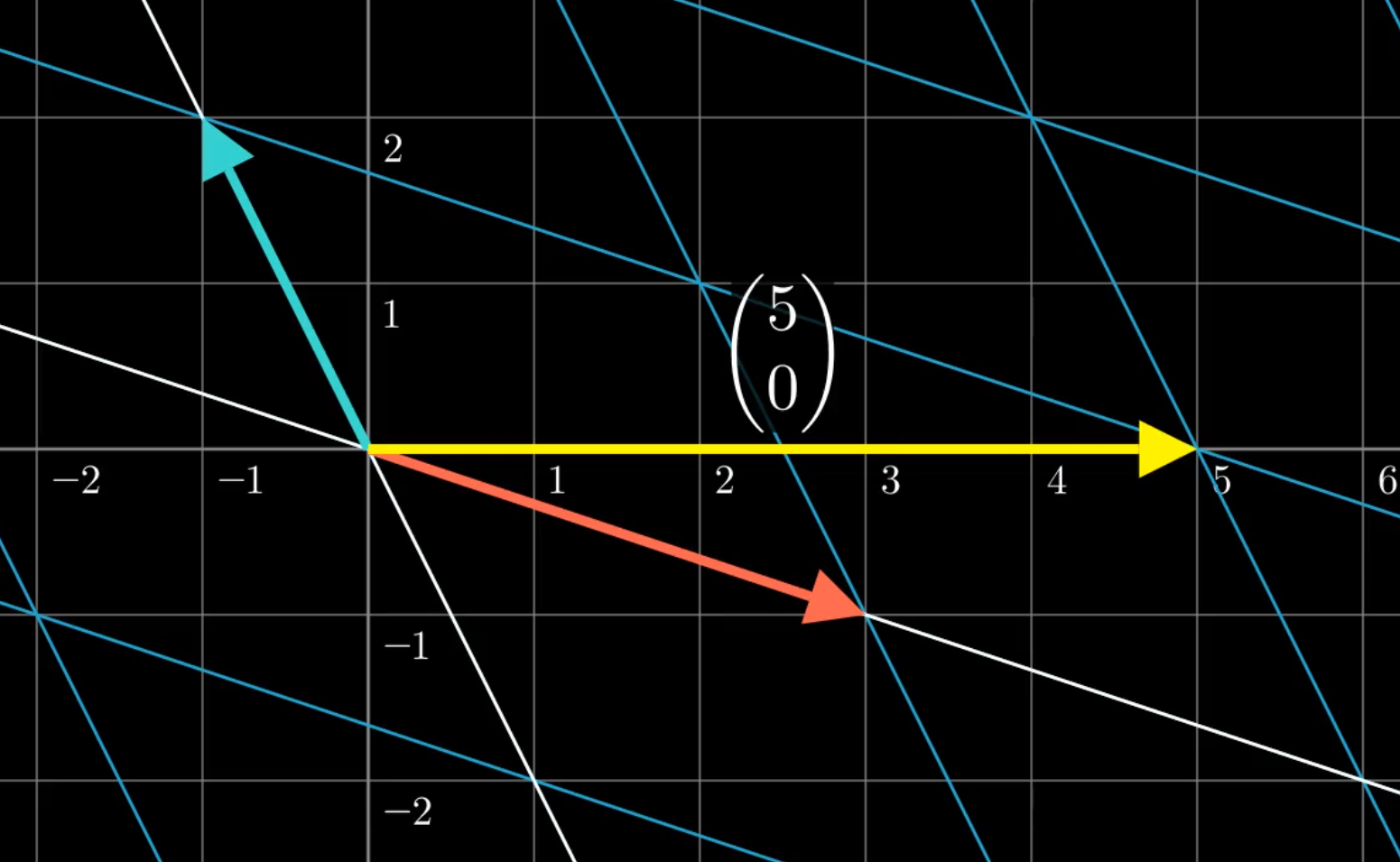
Der gesuchte Vektor ergibt sich abermals aus der Addition von zwei Kopien des ersten Basisvektors und einer Kopie des zweiten Basisvektors – nur dass nach der linearen Abbildung die Basisvektoren andere sind.

Dreht man den ersten Vektor des Skalarprodukts “auf die Seite” (mathematisch sagt man transponieren), so kann man das Resultat als Matrix-Vektor-Produkt interpretieren. Rechnerisch sind Skalarprodukt und Matrix-Vektor-Produkt praktisch identisch:

$$\begin{aligned} \text{Skalarprodukt:} &\quad \begin{pmatrix}3\\4\end{pmatrix} \cdot \begin{pmatrix}2\\1\end{pmatrix} = 3 \cdot 2 + 4 \cdot 1 = 10 \\\ \text{Matrix-Vektor-Produkt:} &\quad \begin{pmatrix} \textcolor{red}{3} & \textcolor{turquoise}{4} \end{pmatrix} \cdot \begin{pmatrix}2\\1\end{pmatrix} = 2 \cdot (\textcolor{red}{3}) + 1 \cdot (\textcolor{turquoise}{4}) = ( 10 ) \end{aligned}$$

Die Matrix $\begin{pmatrix} 3 & 4 \end{pmatrix}$ drückt eine lineare Abbildung von $\mathbb{R}^{2}$ nach $\mathbb{R}$ aus, also von einer zweidimensionalen Fläche auf eine eindimensionale Gerade. Die gesamte Ebene wird gewissermaßen auf eine Zahlengerade “zusammengequetscht” – und zwar so, dass der Basisvektor $\begin{pmatrix} 1 \\ 0 \end{pmatrix}$ auf die Zahl $3$ geschickt wird und der Basisvektor $\begin{pmatrix} 0 \\ 1 \end{pmatrix}$ auf die Zahl $4$.

Nur warum das Ganze?

Wir werden im Folgenden zeigen, dass die lineare Abbildung, die entsteht, wenn man wie oben den ersten Vektor des Skalarprodukts transponiert, genau dieselben Eigenschaften hat, die auch das Skalarprodukt hat. Aufgefasst als lineare Abbildung erklärt sich so also, warum die beiden Darstellungsarten des Skalarprodukts äquivalent sind – sie beschreiben denselben Prozess. Einmal algebraisch, einmal geometrisch.

Um zu verstehen, warum die lineare Abbildung $\begin{pmatrix} 3 & 4 \end{pmatrix}$ tatsächlich die gewünschten Skalarprodukt-Eigenschaften Projektion und Streckung hat, gehen wir Schritt für Schritt vor und schauen zunächst nur auf die Projektion.

Legen wir eine Gerade in das zweidimensionale Koordinatensystem, die in Richtung des Vektors $\begin{pmatrix}3\\4\end{pmatrix}$ verläuft. Untersuchen wir nun die lineare Abbildung, die alle Punkte der Ebene auf diese Gerade projiziert.

Um diese Abbildung mithilfe einer Matrix auszudrücken, müssen wir, wie oben gesehen, lediglich herausfinden, auf welche Vektoren die Abbildung die beiden Basisvektoren $\vec{e}_{1}$ und $\vec{e}_{2}$ schickt.

Da wir ihn gleich brauchen werden, bestimmen wir an dieser Stelle den Einheitsvektor $\vec{u}$ auf der Geraden, d. h. denjenigen Vektor auf der Geraden, der von der $0$ bis zur $1$ geht. Da der Vektor $\begin{pmatrix} 3 \\ 4 \end{pmatrix}$ die Länge $5$ hat, ist der entsprechende Einheitsvektor ein Fünftel so lang: $\vec{u} = \frac{1}{5} \cdot \begin{pmatrix} 3 \\ 4 \end{pmatrix} = \begin{pmatrix} {}^3{\mskip -5mu/\mskip -3mu}_5 \\ {}^4{\mskip -5mu/\mskip -3mu}_5 \end{pmatrix}$.

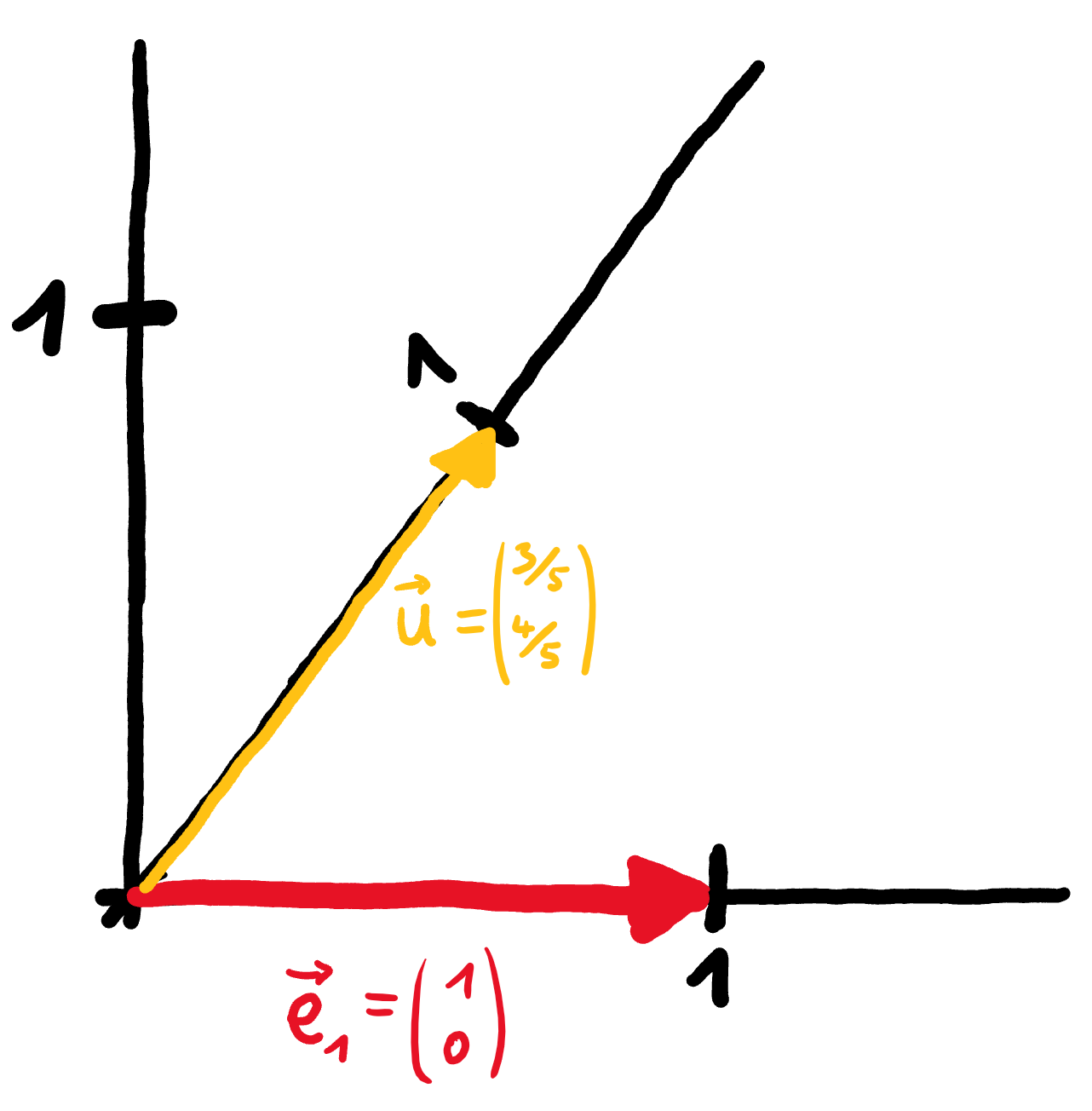
Projizieren wir nun also zunächst $\vec{e}_{1}$ auf die Zahlengerade:

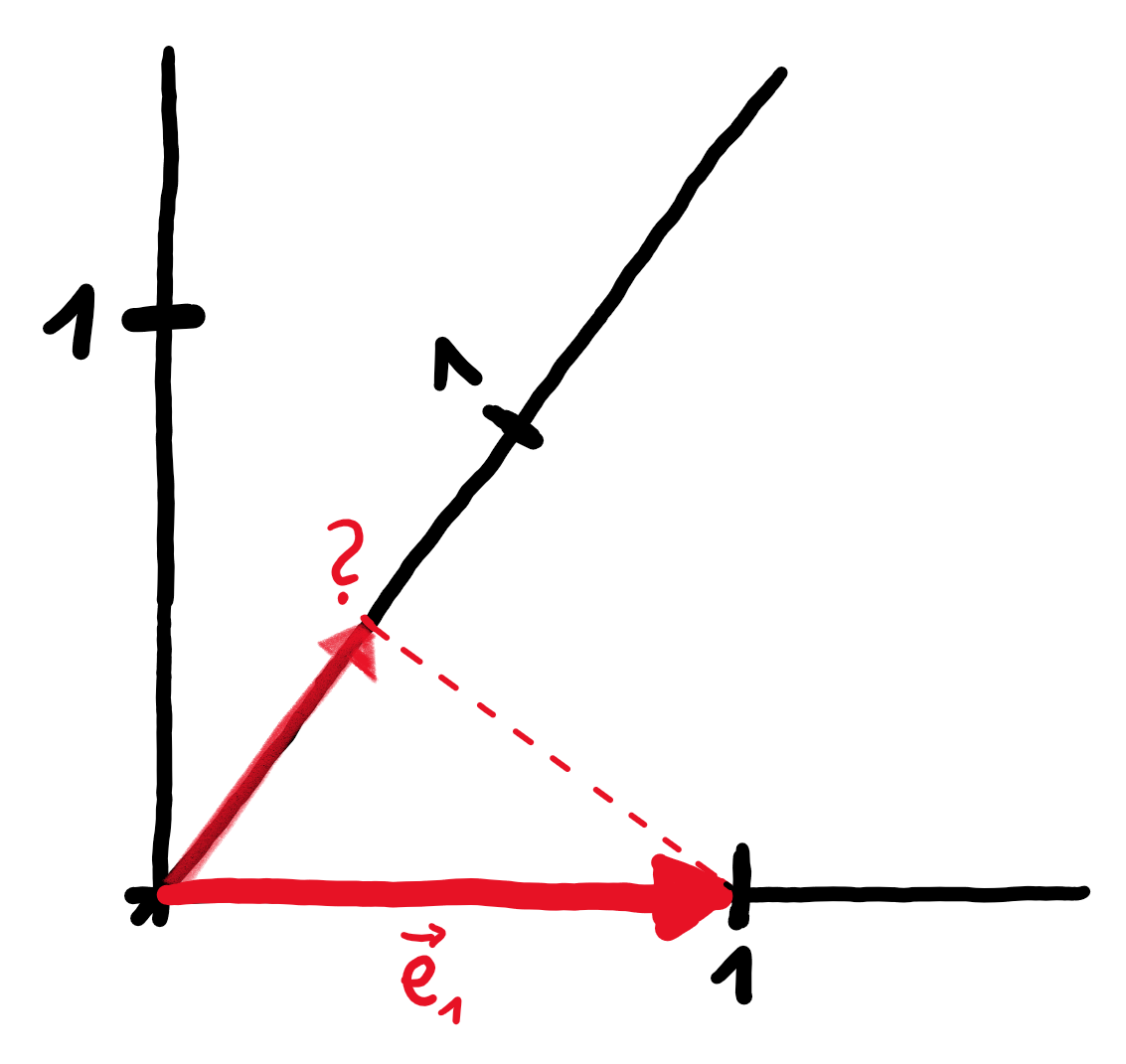
Der Basisvektor $\vec{e}_{1}$ wird auf eine Zahl auf der Zahlengeraden projiziert. Um diese zu bestimmen, nutzen wir ein wundervolles Symmetrieargument.

Jetzt kommt unser zuvor berechneter Vektor $\vec{u}$ ins Spiel. Da beide Vektoren $\vec{e}_{1}$ und $\vec{u}$ die Länge $1$ haben, sieht die Projektion von $\vec{e}_{1}$ auf die Zahlengerade komplett symmetrisch aus zur Projektion von $\vec{u}$ auf die $x$-Achse.

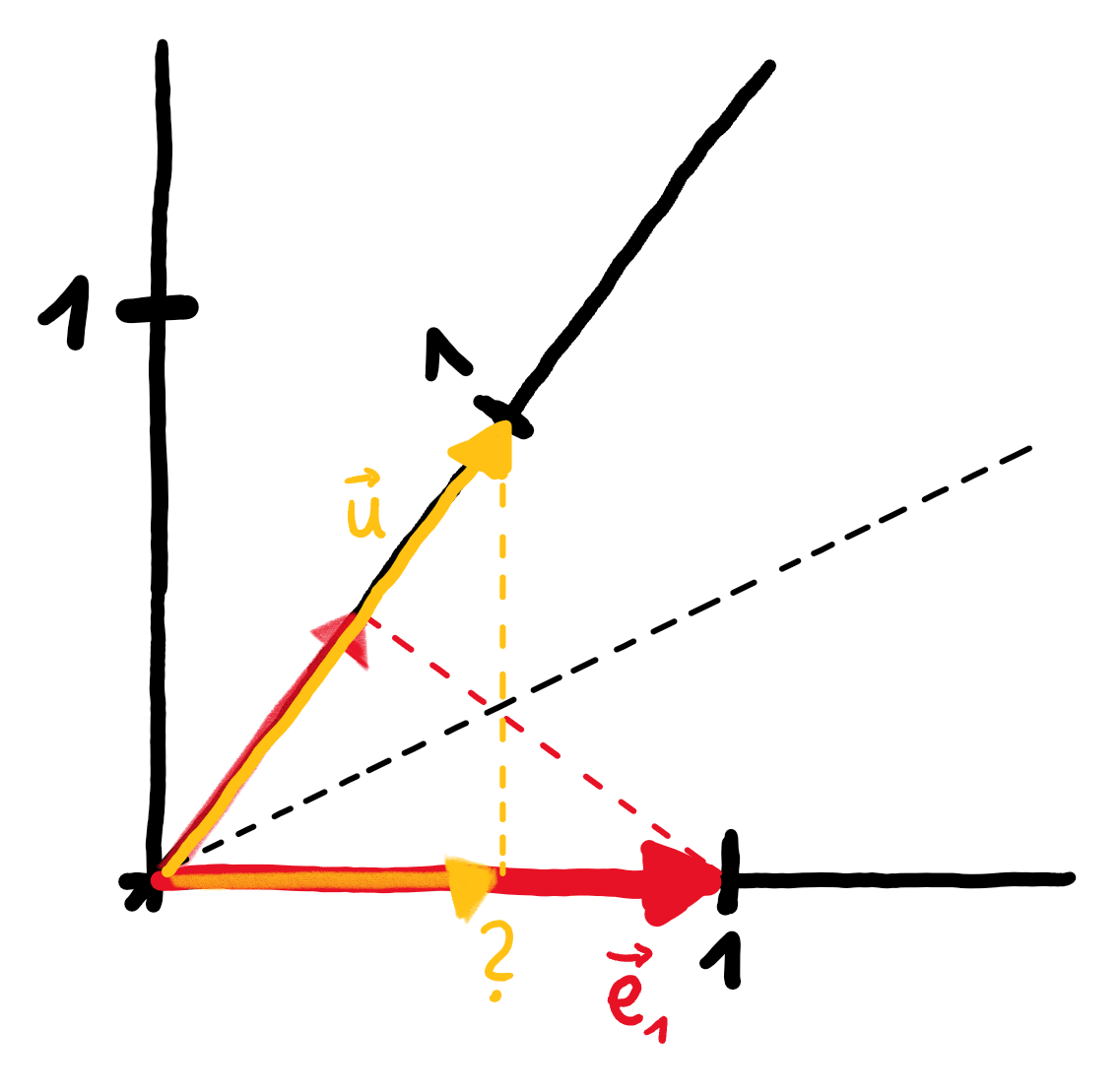
Wenn wir also herausfinden, auf welche Zahl $\vec{u}$ auf der $x$-Achse projiziert wird, wissen wir auch auf welche Zahl $\vec{e}_{1}$ auf der Zahlengeraden projiziert wird.

Die Zahl auf die $\vec{u}$ projiziert wird, ist allerdings einfach die $x$-Koordinate von $\vec{u}$; also ${}^3{\mskip -5mu/\mskip -3mu}_5$. Der Basisvektor $\vec{e}_{1}$ wird also auf ${}^3{\mskip -5mu/\mskip -3mu}_5$ abgebildet.

Mit dem gleichen Symmetrieargument lässt sich zeigen, dass $\vec{e}_{2}$ auf ${}^4{\mskip -5mu/\mskip -3mu}_5$ abgebildet wird.

Die Matrix, die die Projektion auf die Zahlengerade in Richtung $\begin{pmatrix} 3 \\ 4 \end{pmatrix}$ beschreibt, ist damit $\begin{pmatrix} {}^3{\mskip -5mu/\mskip -3mu}_5 & {}^4{\mskip -5mu/\mskip -3mu}_5 \end{pmatrix}$.

Dies entspricht dem transponierten Einheitsvektor $\vec{u}$.

Als kurzen Realitycheck schauen wir uns einmal an, was mit unserem Vektor $\begin{pmatrix}2\\1\end{pmatrix}$ passiert.

Rechnerisch gilt:

$$\begin{pmatrix} \textcolor{red}{{}^3{\mskip -5mu/\mskip -3mu}_5} & \textcolor{turquoise}{{}^4{\mskip -5mu/\mskip -3mu}_5} \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix} = 2 \cdot \left(\textcolor{red}{{}^3{\mskip -5mu/\mskip -3mu}_5}\right) + 1 \cdot \left(\textcolor{turquoise}{{}^4{\mskip -5mu/\mskip -3mu}_5}\right) = ( 2 )$$

Der Vektor müsste also nach der Projektion auf die Zahlengerade auf der $2$ landen.

Multipliziert man eine Abbildungsmatrix mit einem Faktor, so entspricht das grafisch einer gleichmäßigen Streckung in alle Richtungen um eben diesen Faktor.

Multiplizieren wir also die Projektionsmatrix $\begin{pmatrix} {}^3{\mskip -5mu/\mskip -3mu}_5 & {}^4{\mskip -5mu/\mskip -3mu}_5 \end{pmatrix}$ mit dem Faktor $5$, so erhalten wir die Matrix für eine Abbildung, die die gesamte Ebene auf die Zahlengerade projiziert und diese dann um den Faktor $5$ streckt:

$$5 \cdot \begin{pmatrix} {}^3{\mskip -5mu/\mskip -3mu}_5 & {}^4{\mskip -5mu/\mskip -3mu}_5 \end{pmatrix} = \begin{pmatrix} 3 & 4\end{pmatrix}$$

Noch einmal: Die Matrix $\begin{pmatrix} 3 & 4 \end{pmatrix}$ beschreibt eine Projektion auf die Zahlengerade, die in Richtung $\begin{pmatrix} 3 \\ 4 \end{pmatrix}$ verläuft, mit einer anschließenden Streckung um den Faktor $5$, also genau der Länge von $\begin{pmatrix} 3 \\ 4 \end{pmatrix}$.

Das ist genau das, was das Skalarprodukt macht!

Den einen Vektor auf den anderen projizieren und anschließend die Länge der Projektion mit der Länge des anderen Vektors multiplizieren.

Wenn wir das Skalarprodukt durch die Brille der linearen Abbildung betrachten, wird klar, dass die zwei vermeintlich vollkommen unzusammenhängenden Darstellungsarten des Skalarprodukts, tatsächlich lediglich unterschiedliche Blickwinkel auf den gleichen Prozess sind. Sie beschreiben auf algebraische bzw. geometrische Art die lineare Abbildung, die entsteht, wenn man einen der beiden Vektoren transponiert und als Abbildungsmatrix auffasst.

An dieser Stelle möchte ich wärmstens die untenstehenden Quellen empfehlen, allen voran das Video von 3blue1brown zum Skalarprodukt, durch das ich zum ersten Mal auf die Dualität von Skalarprodukt und linearen Abbildungen aufmerksam geworden bin.

Math Stackexchange: Algebraischer Beweis

Gregory Gundersen: Two Forms of the Dot Product

3blue1brown (YouTube): Dot products and duality | Chapter 9, Essence of linear algebra

• Alle
• Math
• Mathe
• Analytische geometrie
• Lineare algebra
• Vektor
• Vector
• Dot product
• Skalarprodukt
• Berechnen
• Cosinus
• 3blue1brown