Entdeckung von Obersumme und Untersumme
# Erarbeitung
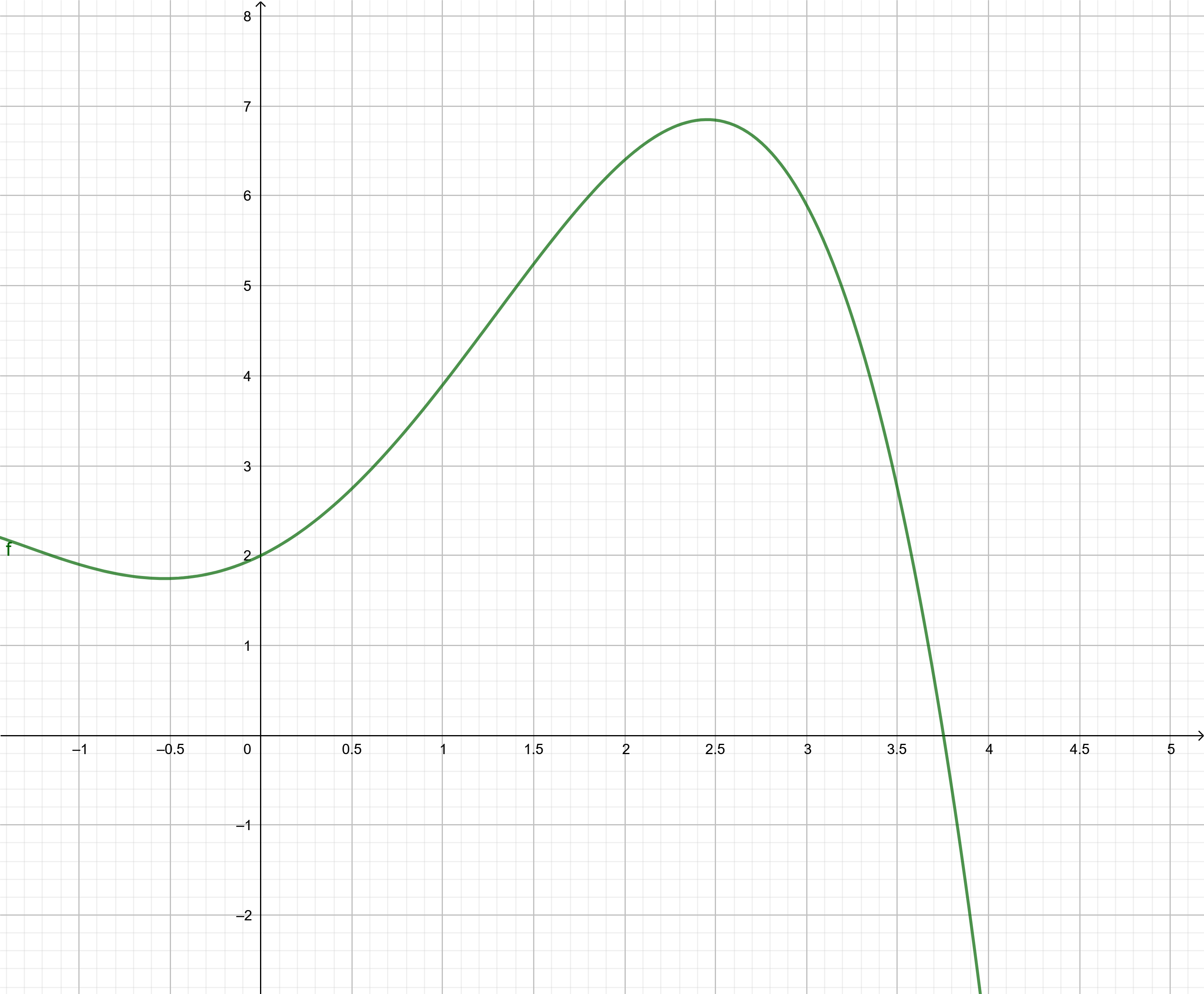
Schüler:innen bekommen ein Bild mit dem Funktionsgraphen von $f(x)=-0,1x^4+x^2+x+2$ und sollen mit den Mitteln, die sie bis jetzt haben, folgendes herausfinden:
- Die möglichst genaue Fläche unter $f$ von $0$ bis $3$.
- Eine Fläche, von der sie sicher sind, dass sie ein bisschen zu klein ist.
- Eine Fläche, von der sie sicher sind, dass sie ein bisschen zu groß ist.
# Sicherung
Ideen der Schüler:innen werden besprochen. Die meisten werden die Fläche angenähert haben mit einfachen Flächen (Rechtecken, Dreiecken).
Unter- und Obersumme werden in Geogebra an $f$ illustriert (Befehle Untersumme & Obersumme).
Weiterführende Frage: Kommt man durch immer feinere Rechtecke auf den genauen Flächeninhalt?