Extremwertaufgaben zur Erarbeitung der Randwertbetrachtung
# Erläuterung
Die folgenden beiden Aufgaben, insbesondere die zweite, sollen der Hinführung der Randwertbetrachtung bei Extremwertproblemen dienen.
In der ersten Aufgabe wird ein globales Maximum gesucht, wobei zunächst die lokalen Extremstellen mit Steigung $0$ berechnet werden. Die Extremstellen an den Rändern werden in der Regel von Schülern nicht weiter beachtet, da diese im konkreten Fall zum einen offensichtlich nicht zum gewünschten Ziel führen und zum anderen die Betrachtung der Randwerte zur Findung von globalen Extremstellen nicht intuitiv klar ist.
In der zweiten Aufgabe ist ein globales Minimum gesucht. Die Berechnung der lokalen Extremstellen mithilfe der notwendigen und hinreichenden Kriterien liefert jedoch nur ein globales Maximum. Zum Finden des globalen Minimums ist deshalb die Betrachtung der Extremstellen an den Rändern notwendig.
# Box basteln
# Aufgabe
Es soll aus einem Blatt DIN A4-Papier durch das Herausschneiden eines Quadrats an jeder Ecke, sowie das anschließende Hochklappen der Seiten eine möglichst große Box gebastelt werden.
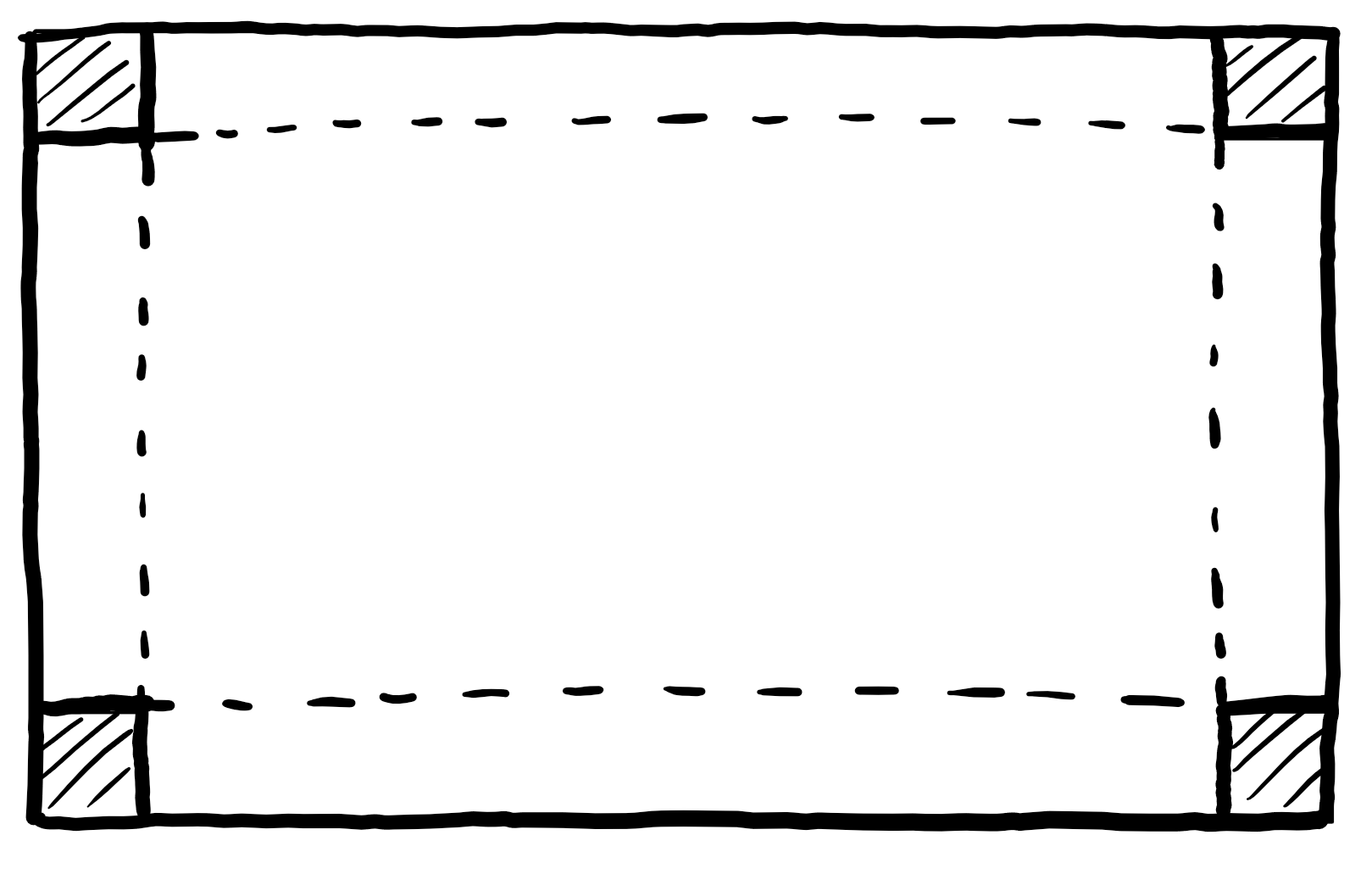
Wie groß müssen die Quadrate sein, damit das Volumen der Box möglichst groß ist?
Hinweis: Im Folgenden wird der Einfachheit halber mit den Seitenlängen $21$ und $30$ gerechnet.
# Lösung
Lösung
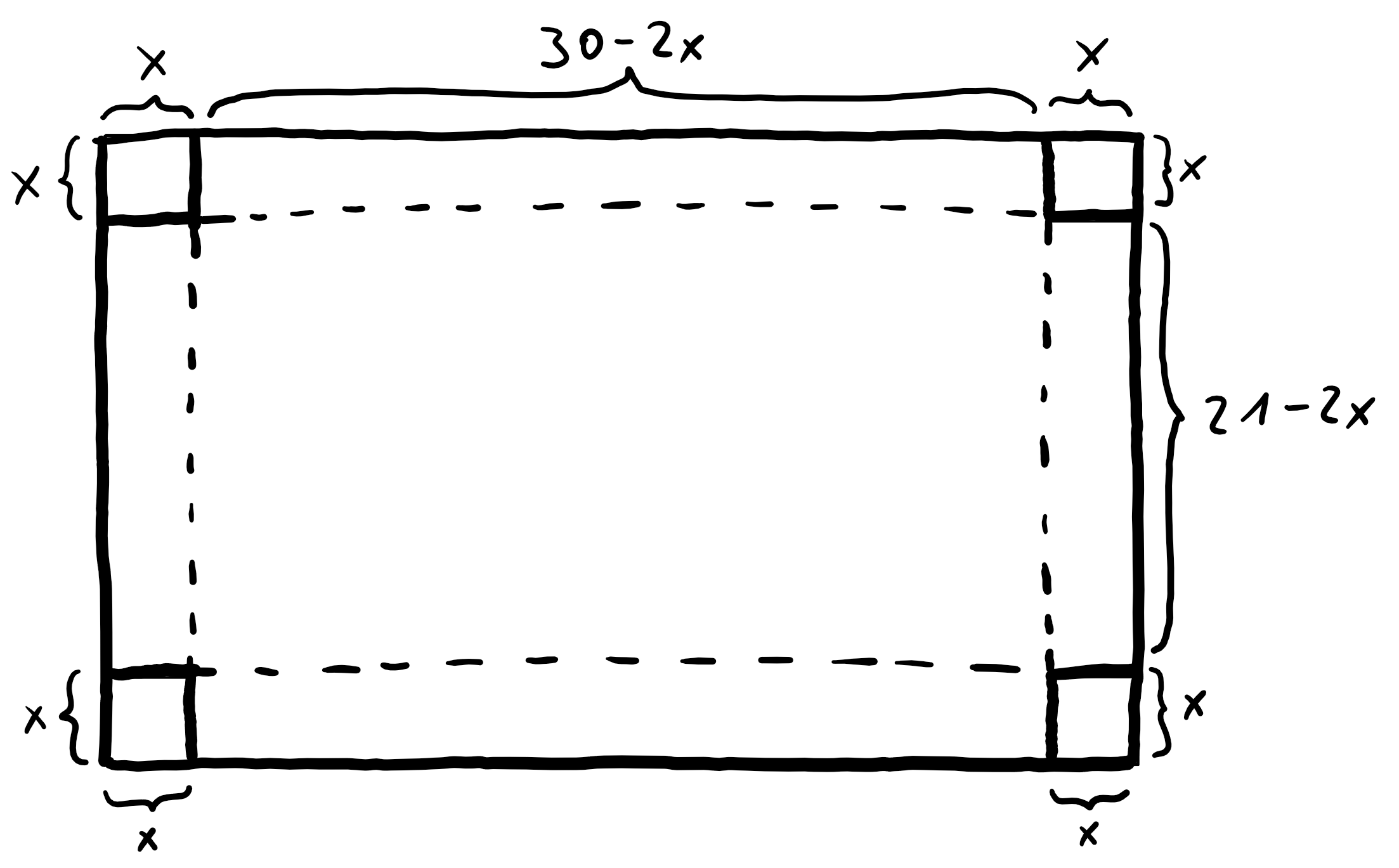
Bezeichnen wir die Länge des Quadrats mit $x$ so ergibt sich folgendes Bild:
Wir können nun eine Funktion $V$ angeben, die das Volumen in Abhängigkeit zur Seitenlänge $x$ des Quadrats angibt:
$$\begin{aligned} V(x) &= x \cdot (21-2x) \cdot (30-2x)\\\ &= 4x^{3}-102x^{2}+630x \end{aligned}$$
Es ist wichtig zu beachten, dass für den Definitionsbereich von $V$ gilt, dass $x \in [0;~10,5]$, da die kürzere Seitenlänge des Blattes $21~cm$ beträgt.
Mithilfe der ersten Ableitung $V’(x)=12x^{2}-204x+630$ die lokalen Extrema berechnen:
$$\begin{aligned} V’(x) &= 0\\\ \Rightarrow x_{1} \approx 4,06&;~~x_{2} \approx 12,94 \end{aligned}$$
Aufgrund des eingeschränkten Definitionsbereichs kommt nur $x_{1}$ als Lösung infrage. Mithilfe der hinreichenden Bedingung zeigt sich, dass sich bei $x_{1}$ in der Tat ein lokaler Hochpunkt befindet.
Nun müssen noch die Randwerte betrachtet werden, die zeigen, dass sich bei $x_{1}$ auch der globale Hochpunkt befindet.
Wenn einem noch kein Beispiel begegnet ist, bei dem die globalen Extrema an den Rändern liegen, wird man den letzten Schritt (Betrachtung der Randwerte) vermutlich nicht durchführen. Das folgende Beispiel dient zur Bewusstmachung, dass die Extrema auch an den Rändern liegen können.
# Kleinstes Rechteck finden
# Aufgabe
Aus einem DIN A4-Blatt wird eine Ecke von je $15~cm$ auf beiden Seiten abgeschnitten.
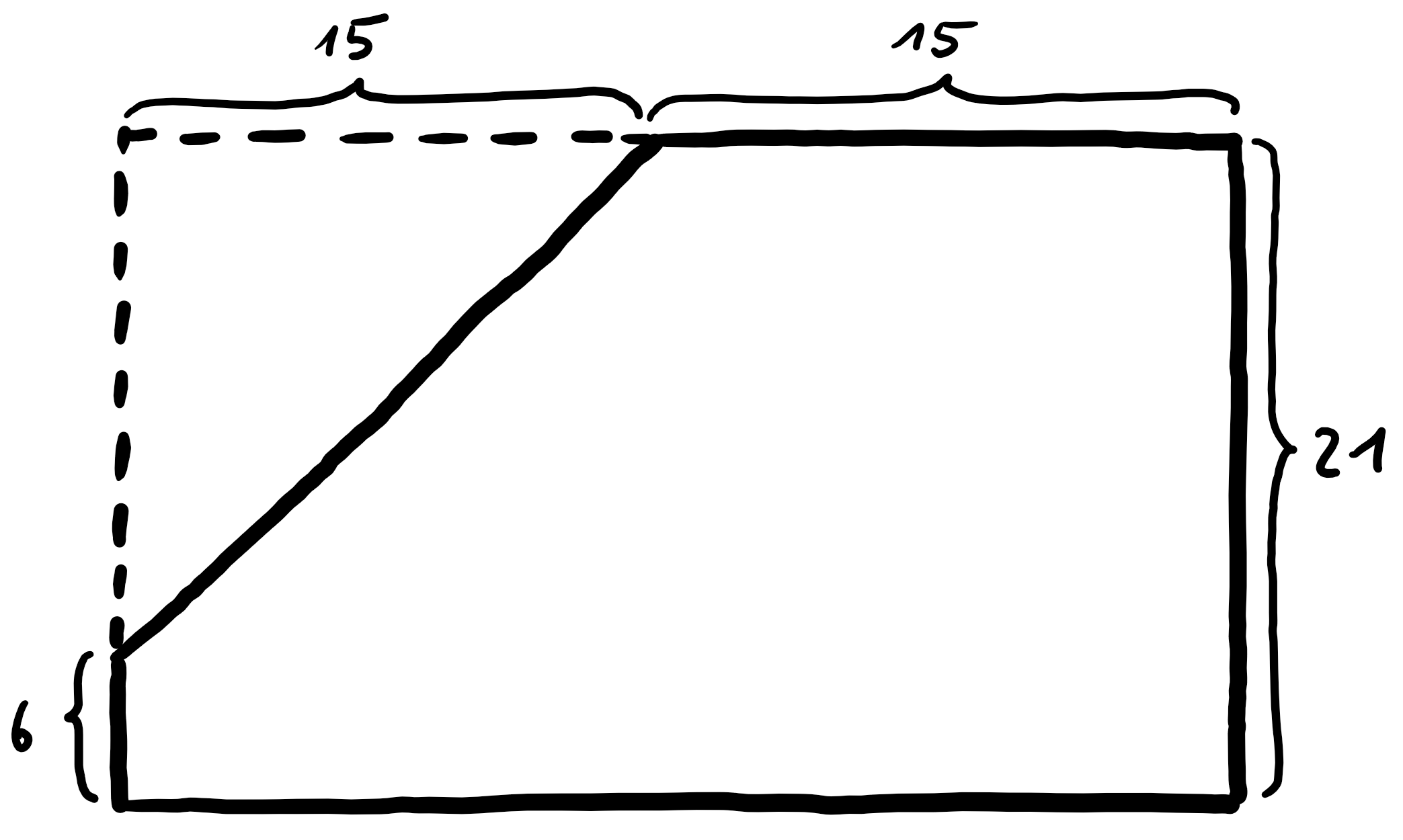
Es soll nun mit zwei Schnitten, welche parallel zu den jeweiligen Seiten verlaufen und sich an der Schrägen treffen, ein neues Rechteck entstehen:
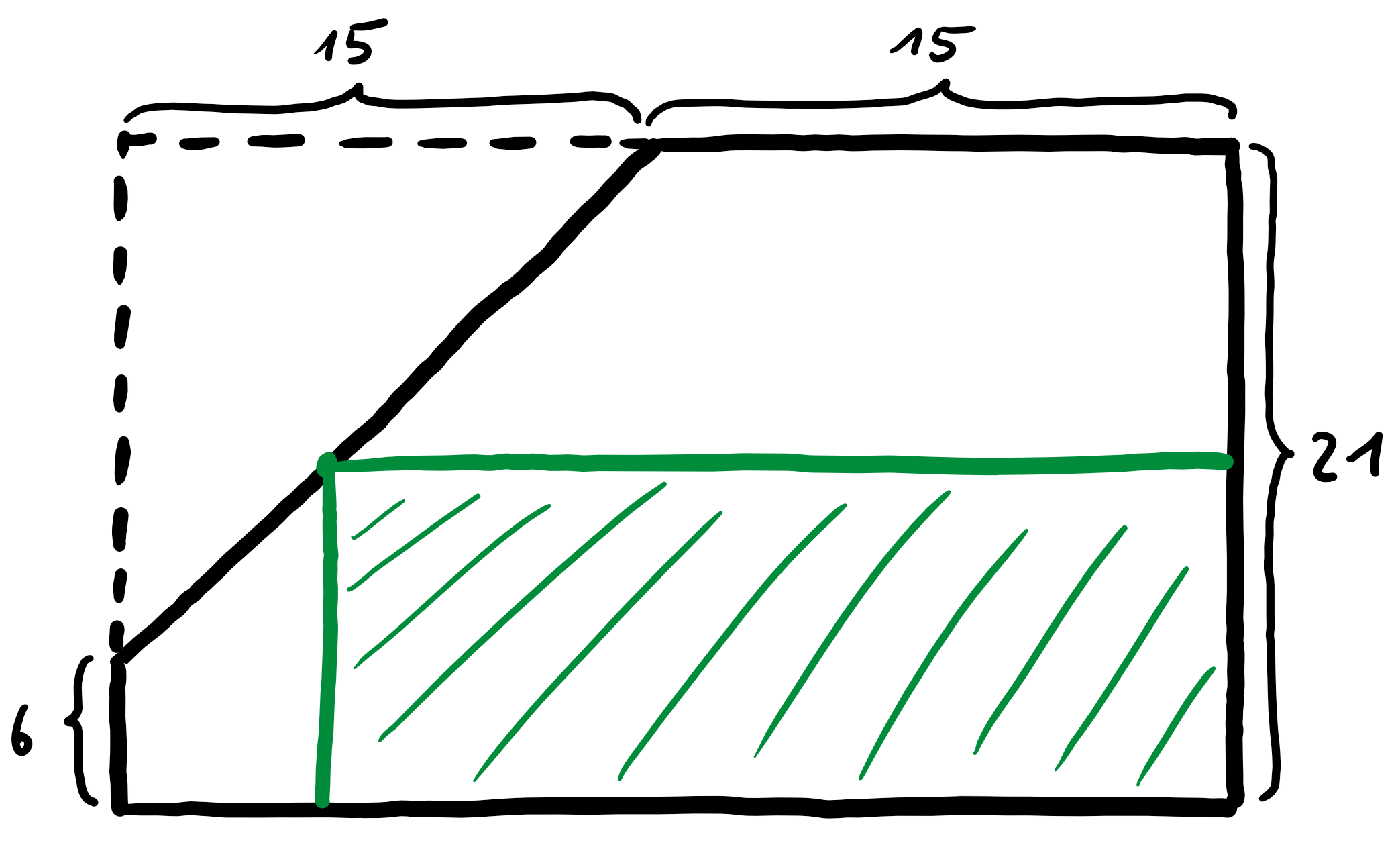
Wo müssen sich die beiden Schnitte treffen, damit das entstehende Rechteck möglichst klein ist?
# Lösung
Lösung
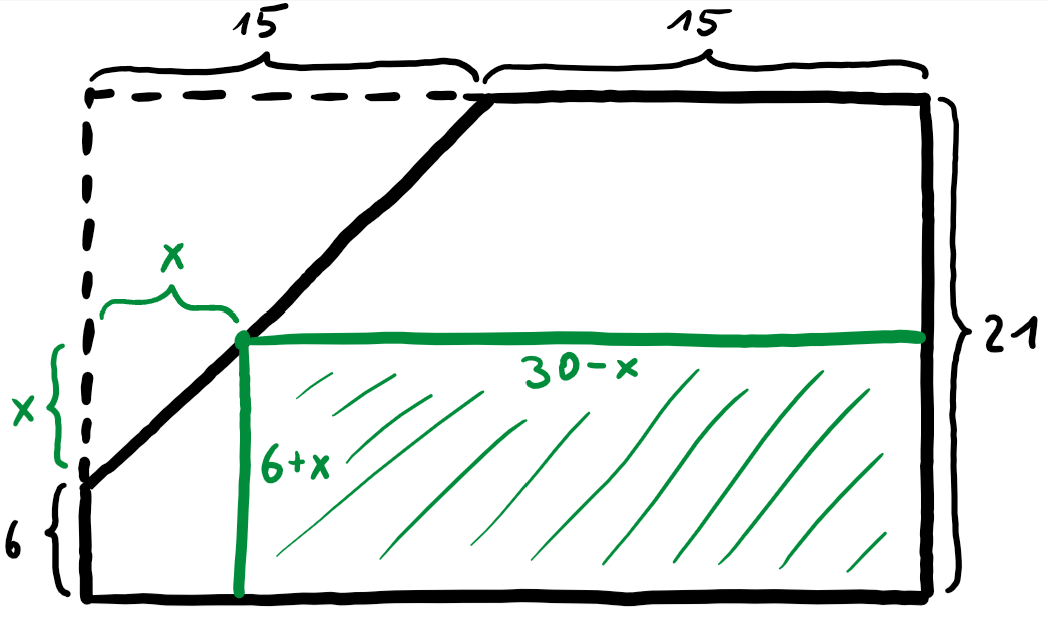
Wir bezeichnen die Seitenlängen des entstehenden Rechtecks wie folgt:
Für den Flächeninhalt $A$ des Rechtecks gilt dann:
$$\begin{aligned} A(x) &= (6+x)(30-x)\\\ &= -x^{2}+24x+180 \end{aligned}$$
Es ist abermals wichtig zu beachten, dass der Definitionsbereich von $A$ eingeschränkt ist. Es gilt, dass $x \in [0;~15]$.
Mithilfe der ersten Ableitung $A’(x)=-2x+24$ die lokalen Extrema:
$$\begin{aligned} A’(x) &= 0\\\ \Rightarrow x &= 12 \end{aligned}$$
Mithilfe der hinreichenden Bedingung zeigt sich, dass sich bei $x=12$ tatsächlich ein lokaler Hochpunkt befindet.
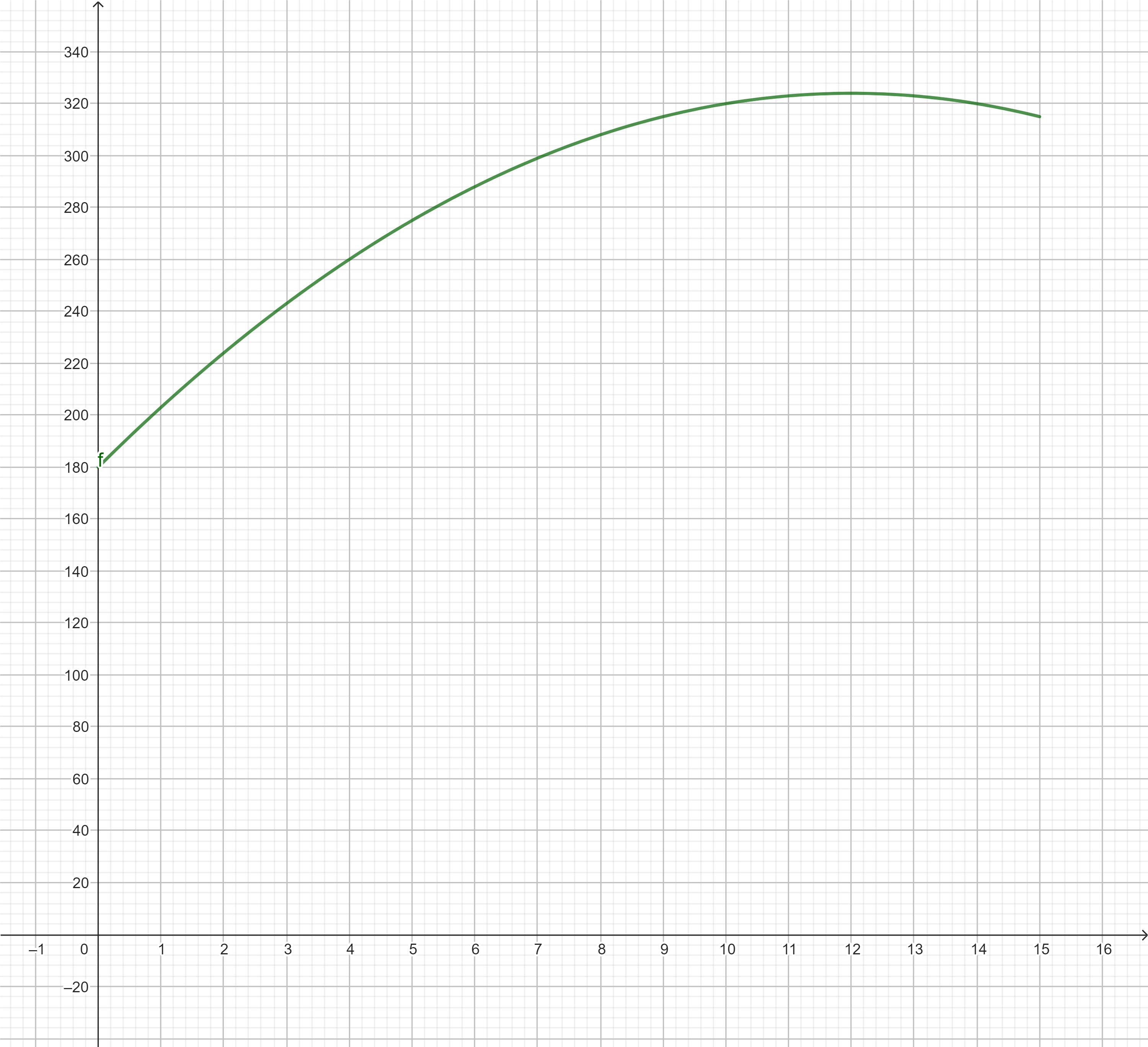
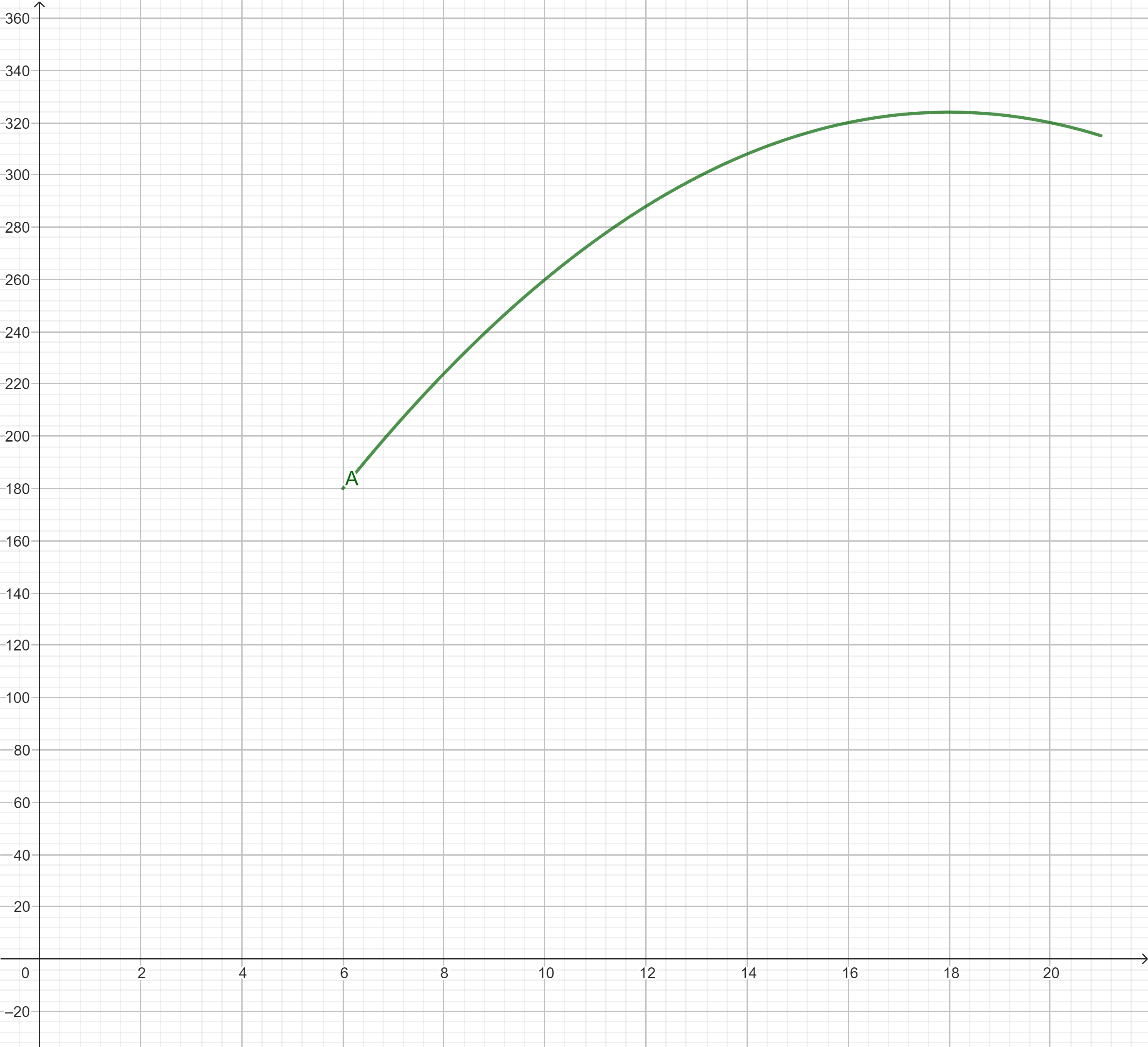
Da wir allerdings nach einem globalen Tiefpunkt suchen, bringt uns diese Entdeckung nicht weiter. Ein Blick auf den Graphen von $A$ zeigt uns, dass der kleinste Wert im Definitionsbereich $[0;~15]$ sich am linken Rand bei $x=0$ befindet.
Das globale Minimum befindet sich an der Stelle $x=0$.
Weiterführende Frage: Warum kann ein globales Extremum nur an den lokalen Extrema oder an den Rändern auftreten?
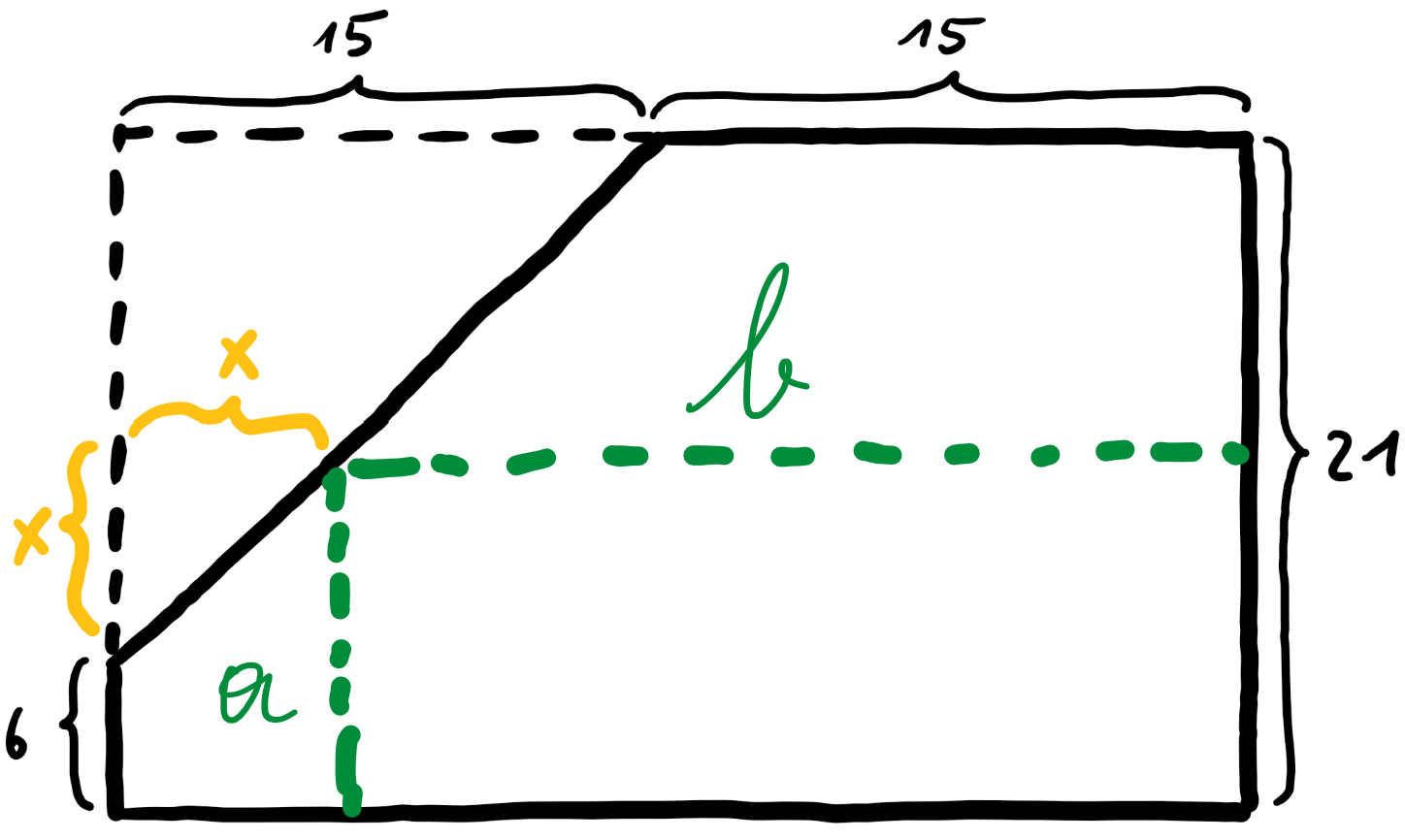
Alternative Lösung
Seien die Seitenlängen des grünen Rechtecks $a$ und $b$. Da der Schnitt in einem 45°-Winkel verläuft, bleibt der Umfang des Rechtecks konstant bei $72$. Denn wenn man die Höhe um eine Länge $x$ verlängert, so verringert sich die Breite um die gleiche Länge $x$.
Für den Flächeninhalt gilt $A=a \cdot b$, für den Umfang gilt $2 \cdot (a+b)=72 \Rightarrow b = 36-a$. Einsetzen in die Flächeninhaltsformel liefert:
$$A(a)=a \cdot (36-a).$$
Die Berechnung der Extremstellen liefert einen Hochpunkt bei $a=18$. Da wir allerdings nach einem Tiefpunkt suchen, bringt uns diese Entdeckung nicht weiter. Ein Blick auf den Graphen von $A$ zeigt uns, dass der kleinste Wert im Definitionsbereich $[6;~21]$ sich am linken Rand bei $a=6$ befindet.
Das globale Minimum befindet sich an der Stelle $a=6$.
Quelle der Lösung: ein LK-Schüler :)