Integration als Gegenteil des Ableitens
# Integration
Der Prozess der Integration nimmt die Information der Steigungen und ermittelt daraus die zugrundeliegende Kurve.
Reiht man alle Steigungen $\frac{\mathrm{d}y}{\mathrm{d}x}$ einer Kurve hintereinander auf, so erhält man eine Reihe von Steigungsdreiecken 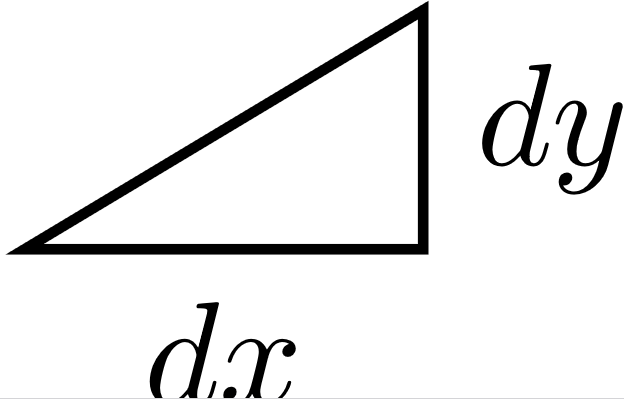 .
.
Zur Veranschaulichung gehen wir von endlichen $\mathrm{d}y$ und $\mathrm{d}x$ aus anstatt von unendlich kleinen.
# Konstante Steigung
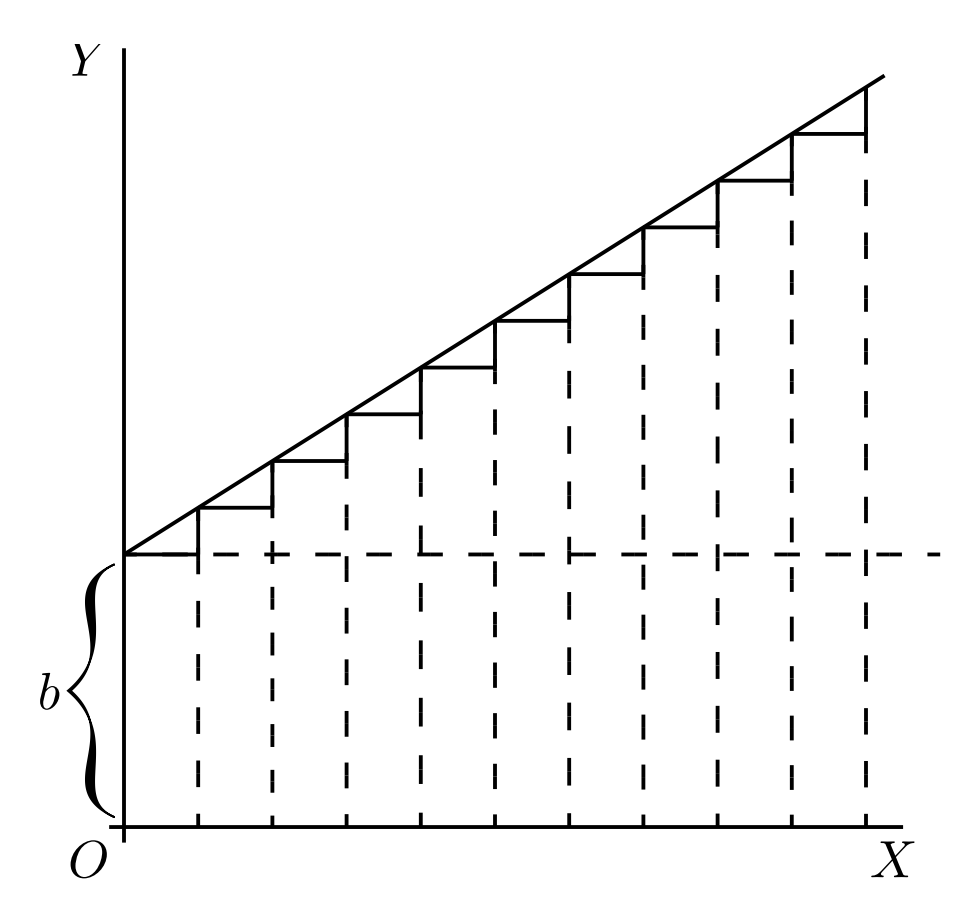
Die Steigung einer unbekannten Kurve $y$ lässt sich als durch die folgenden Steigungsdreiecke mit jeweils einer konstanten Steigung $\frac{\mathrm{d}y}{\mathrm{d}x}=a$ beschreiben:

Wie sieht die Kurve aus, die durch die obigen Steigungen beschrieben wird?
Antwort
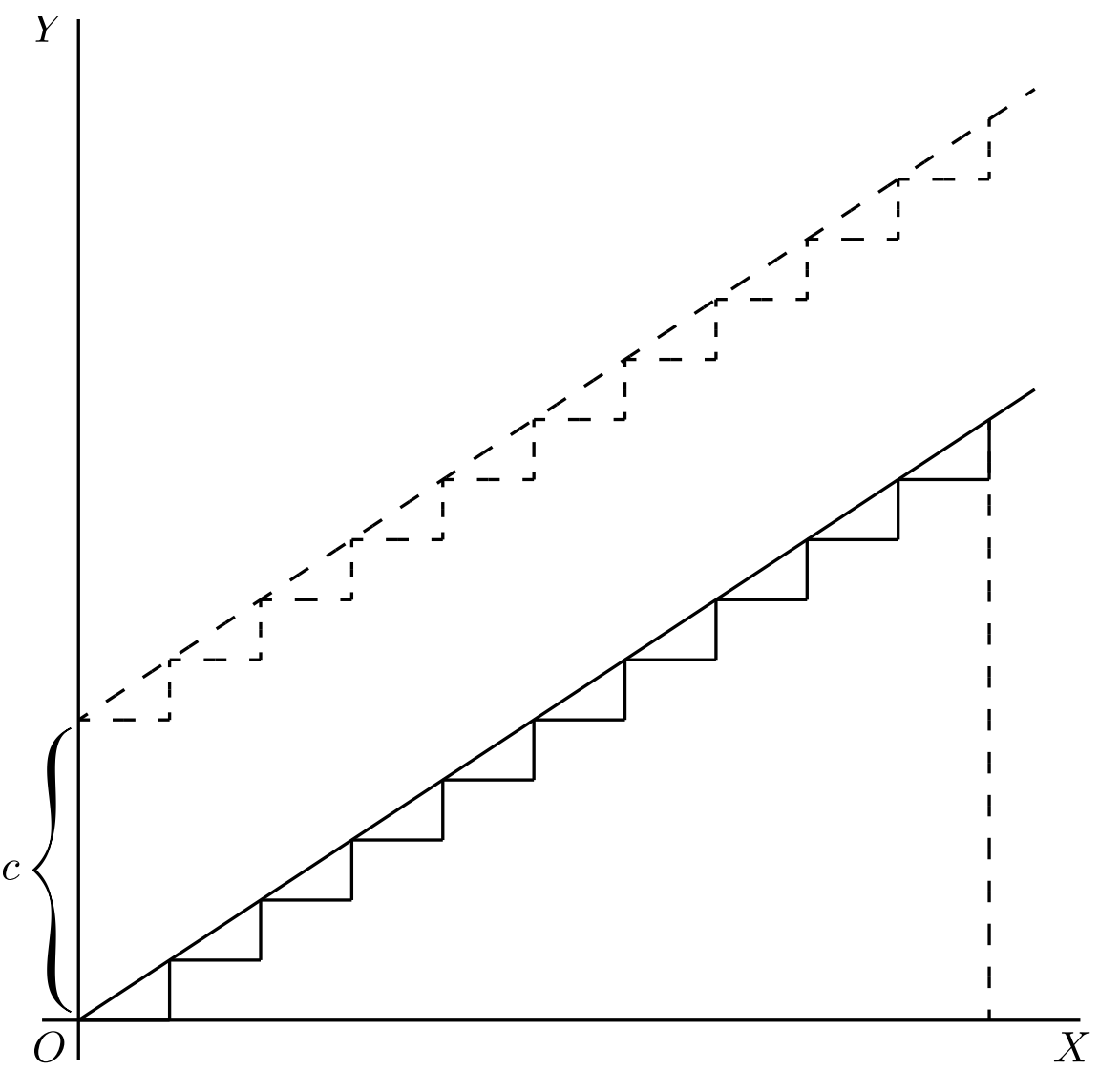
Setzen wir die Dreiecke passend aneinander, so ergibt sich eine Gerade, die durch die lineare Funktion $y=ax+b$ beschrieben wird.
Da die Steigung an jeder Stelle gleich ist, ist es sogar egal, ob die Steigungsdreiecke nun endlich oder unendlich klein sind.
Die Steigungsdreiecke geben jedoch keinen Aufschluss darüber, wo der $y$-Achsenabschnitt der Geraden liegen soll. Dieser ist in gewisser Weise beliebig, da wir nur Informationen über die Steigung haben und eine Änderung des $y$-Achsenabschnitts der Geraden nichts an der Steigung ändert.
Üblicherweise weist man auf diesen Umstand mit einer Konstanten $C$ hin:
$$y=ax+C$$
# Nichtkonstante Steigung
Nehmen wir jetzt an, dass die Steigung einer uns unbekannten Kurve durch $\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{5}x$ gegeben ist. An verschiedenen $x$-Werten ergeben sich nun folgende Steigungen:
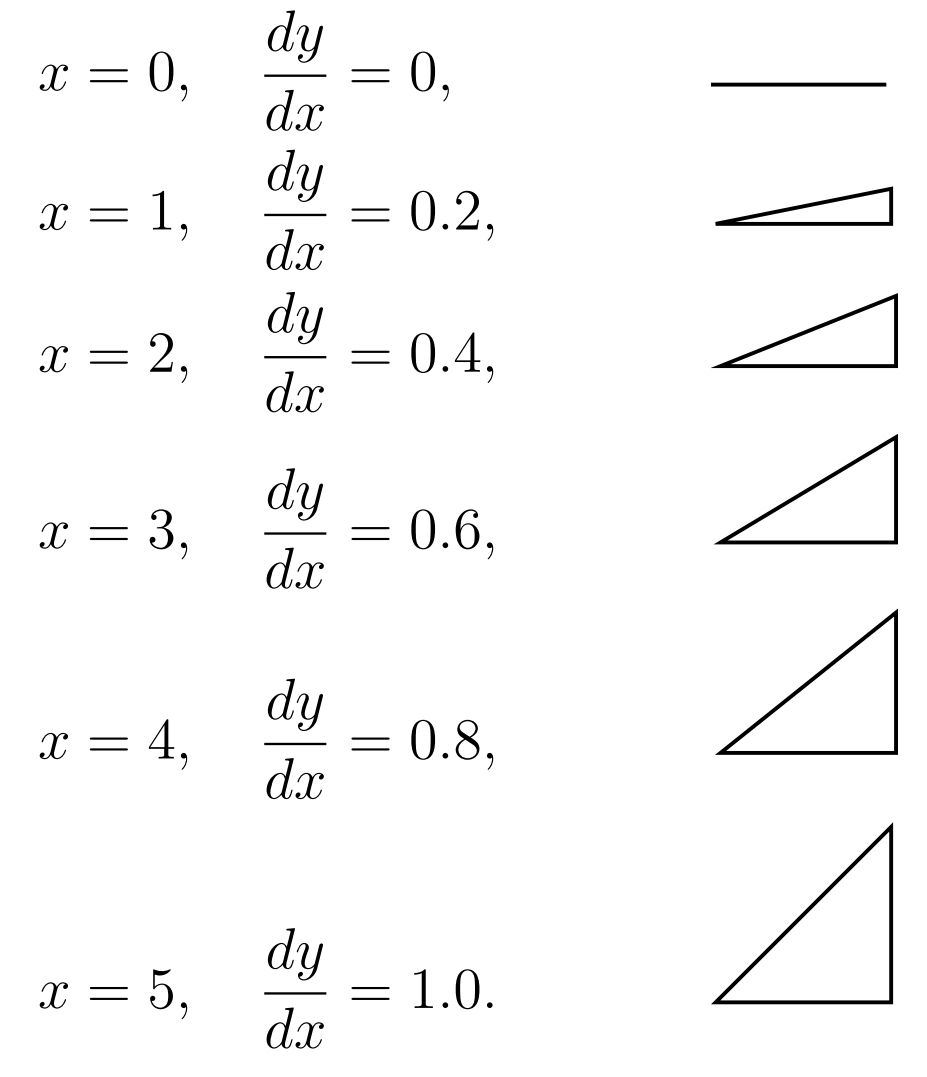
Wie sieht die Kurve aus, die durch die obigen Steigungen beschrieben wird?
Antwort
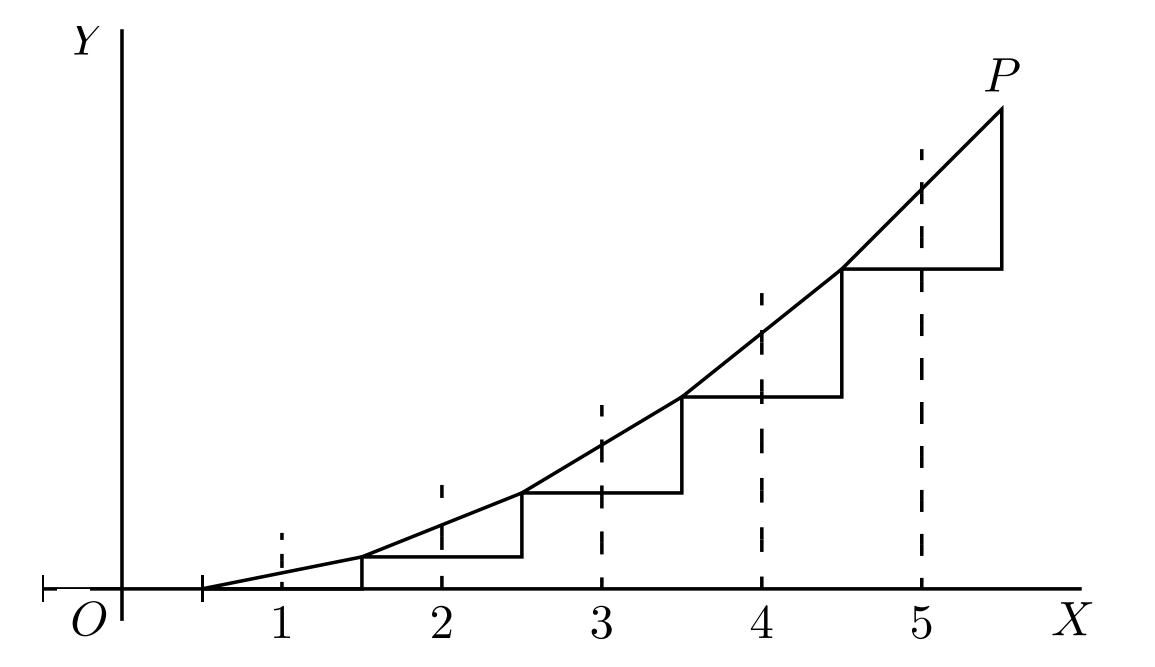
Setzt man die obigen Steigungsdreiecke aneinander, so ergibt sich folgende Kurve:
Dies ist zwar keine “glatte” Kurve, jedoch wird diese durch immer kleiner werdende $\mathrm{d}x$ und $\mathrm{d}y$ beliebig “glatt”.
# Integralschreibweise
Welche Gleichung beschreibt wohl den Verlauf dieser Kurve $y$?
Die Höhe $y$ an einer beliebigen Stelle ergibt sich durch die Summe aller kleinen $\mathrm{d}y$ bis zu dieser Stelle, also $$y=\int\mathrm{d}y.$$
Wegen $$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{5}x$$ $$\Rightarrow \mathrm{d}y=\frac{1}{5}x \cdot \mathrm{d}x$$
gilt:
$$y=\int \frac{1}{5}x~\mathrm{d}x.$$
Die Kurve $y$ ist genau die Kurve, deren Steigung durch $\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{5}x$ beschrieben wird. Nach ein wenig Tüfteln oder beim “Rückwärtsrechnen” der Ableitungsregeln findet man:
$$y=\frac{1}{10}x^{2}.$$
Da abermals nichts über den $y$-Achsenabschnitt bekannt ist und dieser an den Steigungen nichts ändern würde, ergibt sich:
$$y=\frac{1}{10}x^{2}+C.$$
Das Integral $\int \frac{1}{5}x~\mathrm{d}x$ beschreibt also den entgegengesetzten Prozess des Ableitens; aus den Steigungen stellt es die ursprüngliche Kurve wieder her.
$$\int \frac{1}{5}x~\mathrm{d}x=\frac{1}{10}x^{2}+C$$
Erstaunlicherweise lassen sich Integrale auch dafür einsetzen, um Flächeninhalte unter Kurven zu bestimmen. Siehe hierzu auch das entsprechende Kapitel in Calculus made easy.