Lokale und globale Extremstellen
Sei im Folgenden $f \colon I \to \mathbb{R}$ eine Funktion von einem Intervall $I$ auf die reellen Zahlen $\mathbb{R}$. Dabei ist $I \subseteq \mathbb{R}$.
# Lokale Extremstellen
Ein lokales Maximum hat $f$ an der Stelle $x_{0}$, wenn es ein Intervall $(a,b)$ gibt, das $x_{0}$ enthält und in dem gilt $f(x) \leq f(x_{0})$ für alle $x \in (a,b) \cap I$.
Das heißt, wenn es ein offenes Intervall gibt, in dem $f(x_{0})$ der größte Wert ist, dann hat $f$ an der Stelle $x_{0}$ ein lokales Maximum.
(Analog für Minima.)
# Globale Extremstellen
Ein globales Maximum hat $f$ an der Stelle $x_{0}$, wenn $f(x) \leq f(x_{0})$ gilt, für alle $x \in I$.
Das heißt, wenn $f(x_{0})$ der größte Wert im gesamten Definitionsbereich ist, dann hat $f$ an der Stelle $x_{0}$ ein globales Maximum.
(Analog für Minima.)
# Randwerte
Falls Teile des Intervalls $(a,b)$ aus dem Definitionsbereich $I$ herausragen, werden diese ignoriert. Wichtig sind nur die Teile des Intervalls $(a,b)$, die auch im Definitionsbereich liegen.
Das bedeutet, dass Randwerte einer Funktion $f$ immer mindestens lokale Extremstellen sind.
# Zusammenfassung
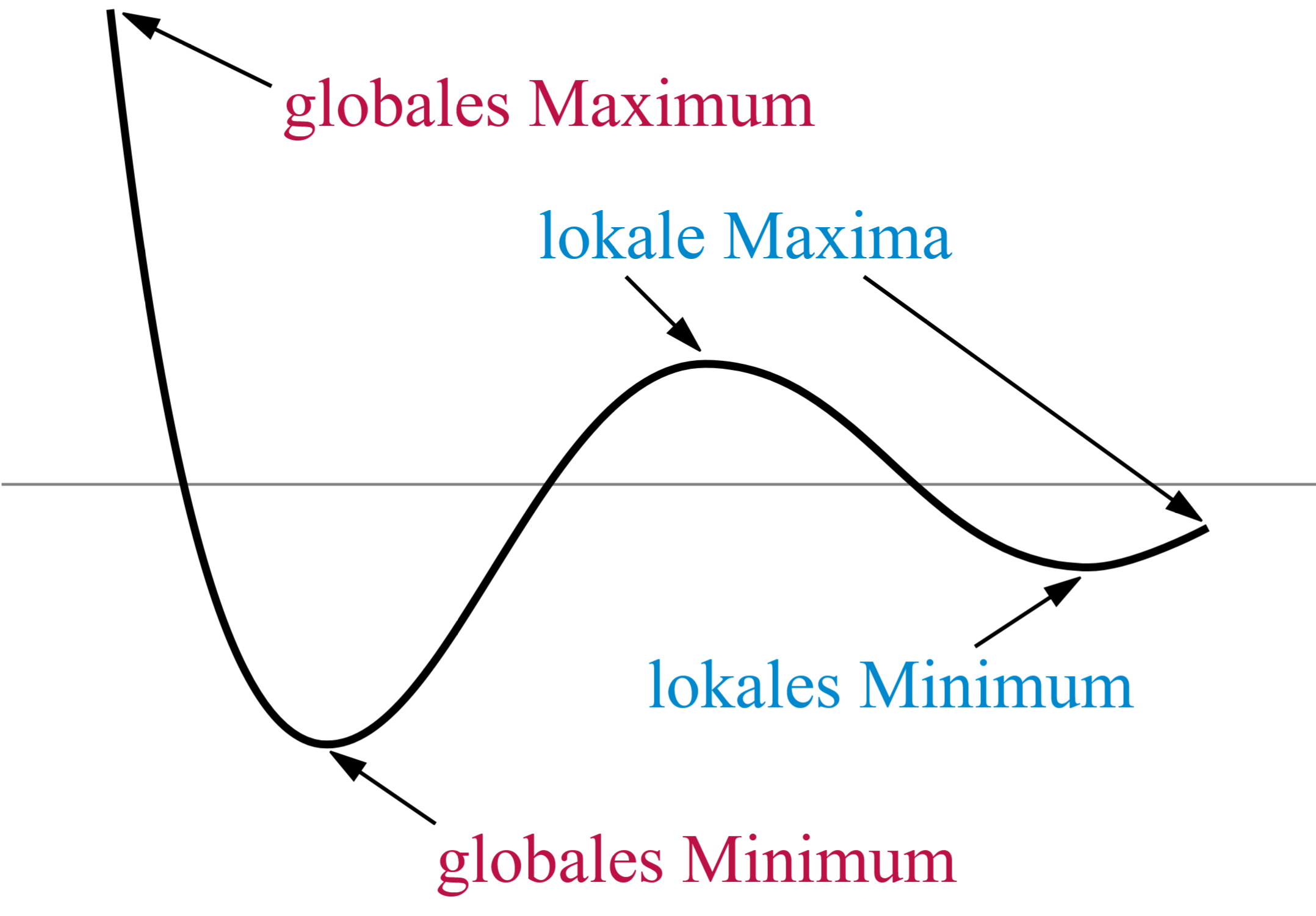
Quelle: https://de.wikipedia.org/wiki/Datei:Extrema_example_de.svg
Weiterführende Frage: Warum kann eine globale Extremstelle nur an den Stellen auftreten, an denen sich lokale Extremstellen befinden?