Ordnung der komplexen Zahlen

Zuletzt aktualisiert Nov 18, 2022 Quelldatei anzeigen

Wir Menschen lieben es, Dinge zu ordnen. 

Wir können zum Beispiel Menschen nach ihrer Größe ordnen, Filme nach ihrer Bewertung oder Gummibärchen nach ihrer Farben. Das macht das Leben organisierter und gibt uns die Möglichkeit, den Dingen um uns herum eine gewisse Struktur zu geben. Aber was genau macht eine Ordnung zu einer Ordnung? Und können wir alles ordnen? 

Und vor allem…lassen sich die komplexen Zahlen $\mathbb{C}$ ordnen? Denn hier ist es z. B. auf den ersten Blick nicht ganz ersichtlich, ob nun die imaginäre Einheit $i$ positiv oder negativ sein soll.

Eine Ordnung ist ein System, das unter den Elementen einer Menge eine bestimmte Reihenfolge etabliert, welche klar definiert, welche Elemente der Menge vor bzw. nach anderen bestimmten Elemente der Menge stehen. $1$ ist z. B. größer als $0$. $2$ ist größer als $1$.
$3$ ist größer als $2$ und so weiter. Mathematisch gesehen können wir sagen: $0 < 1 < 2 < 3 < \ldots$ Von hier an werden wir das Symbol $\leq$ (kleiner gleich) zum Vergleichen zweier Elemente verwenden. Diese Forderung ist nicht so streng wie $<$ und reicht zum Ordnen völlig aus.

Was muss eine Ordnung nun eigentlich leisten, um als Ordnung bezeichnet zu werden?

Nun, es gibt vier Eigenschaften, die wir von einer Ordnung fordern wollen. Einige davon mögen völlig offensichtlich erscheinen, sind aber dennoch notwendig, um die gesamte Bandbreite der Fälle abzudecken, in denen wir eine Ordnung verwenden möchten. Die folgenden vier Axiome (Aussagen, die wir offensichtlich für wahr befinden und die nicht weiter bewiesen werden müssen) legen fest, wie sich unsere $\leq$-Beziehung beim Vergleich von Elementen verhalten soll:

$(\rm i)\quad a \leq a$
(Reflexivität = ein Element ist immer kleiner gleich sich selbst)

$(\rm ii)\quad a \leq b ~~~~\text{oder}~~~~ b \leq a$
(Totalität = jedes Paar von Elementen ist vergleichbar)

$(\rm iii)\quad \text{Wenn}~~ a \leq b ~~\text{und}~~ b \leq a, ~~\text{dann ist}~~ a=b$ 
(Antisymmetrie = entweder ist ein Element kleiner als das andere oder beide gleich groß)

$(\rm iv)\quad \text{Wenn}~~ a \leq b ~~\text{und}~~ b \leq c, ~~\text{dann ist}~~ a \leq c$ 
(Transitivität = kein “Schnick-Schnack-Schnuck”)

Ich wette, die Axiome $(\rm i)$ bis $(\rm iii)$ scheinen ziemlich einleuchtend oder gar trivial zu sein. Axiom $(\rm iv)$ besagt, dass wir keine Schleifen wie beim Spiel Schnick-Schnack-Schnuck wollen, sondern dass, wenn $b$ größer gleich $a$ ist und $c$ größer gleich $b$ ist, dass dann auch $c$ größer gleich $a$ sein muss. So wie wir sagen, dass $3$ größer als $2$ und $2$ größer als $1$ ist und das deswegen auch $3$ größer als $1$ sein muss.

Auch wenn dies bei Zahlen offensichtlich erscheinen mag, ist diese Logik in Wirklichkeit überhaupt nicht die Regel. Hierzu empfehle ich dieses großartige Numberphile-Video mit Tadashi Tokieda, in dem er einen Satz von nicht-transitiven Würfeln zeigt, welche sich genau wie bei Schnick-Schnack-Schnuck gegenseitig im Kreis schlagen.

Und das ist nun alles, was wir brauchen. Wenn wir eine Art von Beziehung zwischen zwei Objekten erfinden, die diese vier Axiome erfüllt, nennen wir diese eine Totalordnung.  Wow, total!

Alles was die obigen vier Axiome erfüllt, kann man also eine Ordnung nennen. Würfeln wir doch deshalb unsere Zahlen einmal willkürlich durch und schauen, was die Axiome sagen.

Würfel, würfel, würfel…tadaaa:

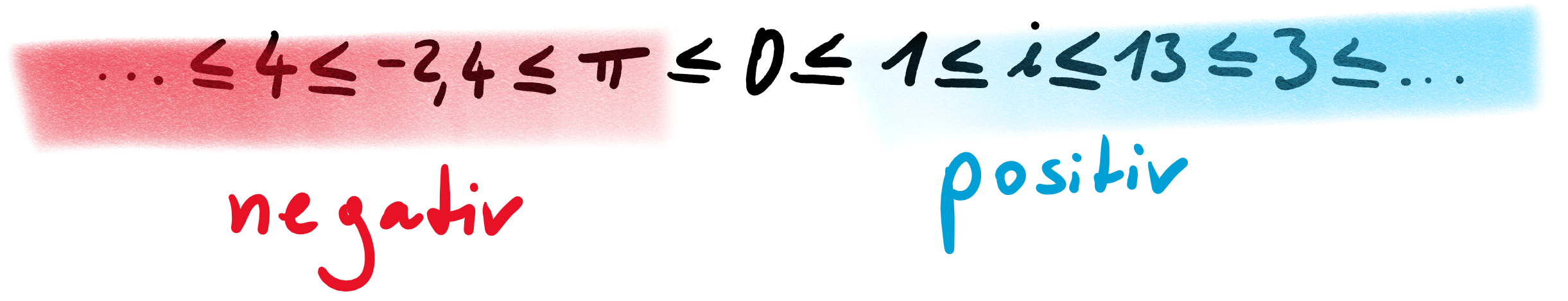
Diese Ordnung der Zahlen ist augenscheinlich ziemlich sinnlos, aber alle unsere Axiome sind erfüllt und damit ist dies tatsächlich eine Ordnung.

Case closed. Die komplexen Zahlen $\mathbb{C}$ lassen sich ordnen. Vielen Dank und tschüüü…Moment!

Ja, man könnte die komplexen Zahlen völlig willkürlich anordnen und dadurch eine Ordnung erhalten, aber das sieht nun so gar nicht mehr aus wie die uns bekannten komplexen Zahlen. Außerdem wollen wir ja auch mit unseren Zahlen wie gewohnt rechnen können.

Schauen wir noch einmal auf unsere obige willkürliche Ordnung so sehen wir, dass wenn wir die beiden positiven Zahlen $1$ & $3$ addieren, die nun negative Zahl $4$ herauskommt. Das darf natürlich nicht sein. Wenn wir zwei positive Zahlen addieren, muss wieder eine positive Zahl herauskommen und vor allem eine, die größer ist, als jede der beiden Zahlen für sich genommen.

In Bezug auf das Rechnen müssen wir für unsere Ordnungen also noch weitere Forderungen aufstellen. Denn eine Ordnung, mit der man nicht mehr vernünftig rechnen kann, ist nicht sonderlich hilfreich.

Wir wollen also, dass wir mit unserer Ordnung auch Rechnen können. Hierfür müssen die folgenden Eigenschaften gelten:

$(\rm v)\quad \text{Wenn}~~ a \leq b, ~~\text{dann ist}~~ a+c \leq b+c$
(Addition)

$(\rm vi)\quad \text{Wenn}~~ a \leq b ~~\text{und}~~ 0 \leq c, ~~\text{dann ist}~~ a \cdot c \leq b \cdot c$
(Multiplikation)

Erfüllt ein Körper mit einer Ordnungsrelation alle 6 vorgestellten Axiome, nennt man ihn einen geordneten Körper.

Die soeben vorgestellten Eigenschaften $(\rm v)$ und $(\rm vi)$ sollen am folgenden Beispiel veranschaulicht werden.

Wenn $Alice$ kleiner ist als $Bob$, …

…dann ist $Alice~mit~Zylinder$ auch kleiner als $Bob~mit~demselben~Zylinder$.

Wenn also $Alice \leq Bob$, dann gilt auch: $Alice + Zylinder \leq Bob + Zylinder$.

Wenn $Alice$ kleiner ist als $Bob$, …

…dann sind auch $3-mal~Alice~übereinander$ kleiner als $3-mal~Bob~übereinander$.

Wenn also $Alice \leq Bob$, dann ist auch $c-mal~Alice \leq c-mal~Bob$.

Wobei $c$ hier eine positive Zahl ist.

Schaffen wir es also nun eine Ordnung für $\mathbb{C}$ zu finden, die alle 6 Axiome erfüllt, dann haben wir eine Ordnung gefunden, die dafür sorgt, dass wir auch weiterhin mit den komplexen Zahlen rechnen können, wie wir es gewohnt sind.

Leider werden wir feststellen, dass egal welche Wahl wir für $i$ treffen, also entweder kleiner gleich $0$ oder größer gleich $0$ (eines von beiden muss sie schließlich sein), wir immer einen logischen Widerspruch erhalten werden.

Die Beweismethode, die wir im folgenden Beweis verwenden, nennt sich Beweis durch Widerspruch. Wir nehmen einfach an, dass es eine totale Ordnung der komplexen Zahlen gibt. Dann muss nach $(\rm ii)$ entweder $0 \leq i$ oder $i \leq 0$ gelten. Wir wissen noch nicht, wo $i$ liegt, entweder kleiner gleich $0$ oder größer gleich $0$.

Nehmen wir an, dass $i$ größer gleich $0$ ist, also $0 \leq i$: 

Nach $(\rm vi)$ bedeutet dies, dass $0 \cdot i \leq i \cdot i \Rightarrow 0 \leq -1$ ist. 

Wenn also $i$ größer gleich $0$ ist, muss auch $-1$ größer gleich $0$ sein. In den uns vertrauten reellen Zahlen wäre dies bereits ein Widerspruch, aber Vorsicht, wir haben es hier mit komplexen Zahlen zu tun. Und soweit wir wissen, könnte deren Reihenfolge völlig anders sein. Und weil nun $0 \leq -1$ gilt, können wir wiederum mit Hilfe von $(\rm vi)$ schließen, dass $0 \cdot (-1) \leq (-1) \cdot (-1) \Rightarrow 0 \leq 1$. Das bedeutet, dass auch $1$ größer gleich $0$ sein muss. 

Betrachtet man jedoch die Tatsache, dass $0 \leq -1$ ist, und addiert $1$ zu beiden Seiten, so muss die linke Seite immer noch kleiner gleich der rechten sein, gemäß $(\rm v)$. Also $0+1 \leq -1+1 \Rightarrow 1 \leq 0$, was bedeutet, dass $1$ kleiner gleich $0$ sein muss.

Wir haben also, dass $0 \leq 1$ und $1 \leq 0$, was nach $(\rm iii)$ bedeutet, dass $0=1$ ist, was jedoch selbst in den komplexen Zahlen eindeutig Unsinn ist. Da wir zu einer Aussage gekommen sind, die falsch ist, muss unsere Annahme, dass $0 \leq i$ ist, falsch gewesen sein.

Nehmen wir also an, dass $i$ kleiner gleich $0$ ist; dass also $i \leq 0$: 

Nach $(\rm v)$ wissen wir, dass $i+(-i) \leq 0+(-i) \Rightarrow 0 \leq -i$.

Da $-i$ größer gleich $0$ ist, ergibt $(\rm vi)$, dass $0 \cdot(-i) \leq (-i) \cdot (-i) \Rightarrow 0 \leq -1$. Von hier an können wir der Argumentationskette aus Fall 1 folgen, um analog zum gleichen Widerspruch zu gelangen.

Der vollständige Beweis, sei in guter mathematischer Tradition dem Leser als Übung überlassen.

Lassen sich die komplexen Zahlen $\mathbb{C}$ ordnen?

Jein.

Die komplexen Zahlen $\mathbb{C}$ lassen sich tatsächlich ordnen (sogar auf beliebige Art und Weise), solange man die Axiome $(\rm i)$ bis $(\rm iv)$ erfüllt. Allerdings ist eine jede solche Ordnung wenig sinnvoll, da wir mit ihr nicht mehr vernünftig rechnen könnten. Egal ob wir $i$ als positiv oder negativ deklarieren, wir werden uns früher oder später in Widersprüche verstricken. Die einzige Lösung für dieses Dilemma ist es, zu sagen: Wenn wir rechnen können wollen, dann können wir $\mathbb{C}$ nicht ordnen.

Wenn man also das nächste Mal den Schlüssel verlegt hat und die eigenen Sachen vor lauter Unordnung nicht mehr wiederfinden kann, kann man sich immerhin damit trösten, dass man ohne diese Unordnung nicht mehr rechnen könnte. Und das will doch nun wirklich keiner ;)

• Alle
• Mathe
• Math
• Komplexe zahlen
• Complex numbers
• Order
• Ordnung
• Axiom
• Größe
• Körper
• Algebra
• Widerspruch
• Beweis
• Proof