Orthogonale Vektoren
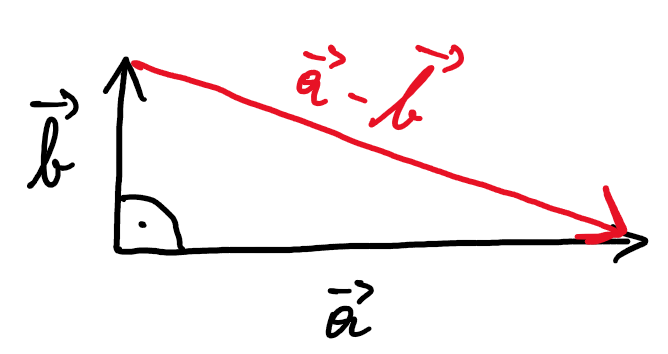
Zwei Vektoren $\vec{a}$, $\vec{b}$ stehen orthogonal aufeinander, wenn sie in einem rechten Winkel zueinander liegen. Man schreibt dann: $\vec{a}\perp\vec{b}$.
Die Orthogonalität kann mithilfe der Koordinaten der Vektoren bestimmt werden. Bei der Herleitung hilft uns der Satz des Pythagoras.
Gegeben seien zwei Vektoren $\vec{a}=\begin{pmatrix}a_{1} \\ a_{2}\end{pmatrix}$ und $\vec{b}=\begin{pmatrix}b_{1} \\ b_{2}\end{pmatrix}$ aus dem $\mathbb{R}^{2}$, d. h. aus dem Zweidimensionalen.
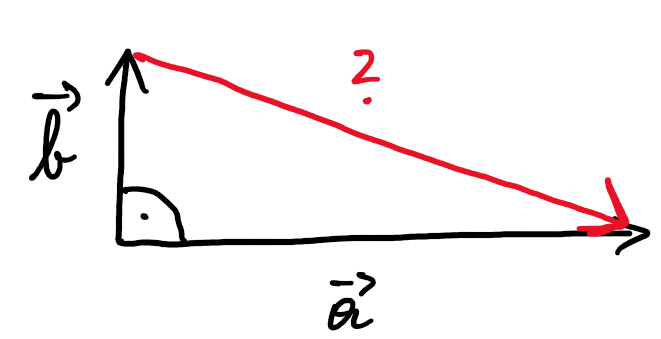
Wie kann der rote Vektor auf der Hypotenuse mithilfe der anderen beiden Vektoren beschreiben?
Antwort
Wir gehen von der Spitze des Vektors $\vec{b}$ zur Spitze des Vektors $\vec{a}$. Dabei gehen wir zuerst in Richtung $-\vec{b}$ und anschließend in Richtung $\vec{a}$. Die gesamte Richtung ist also $-\vec{b}+\vec{a}$ oder auch $\vec{a}-\vec{b}$.
Alternativ könnte der Hypotenusenvektor auch in die entgegengesetzte Richtung laufen, also von der Spitze von $\vec{a}$ zur Spitze von $\vec{b}$. Das entspräche dem Vektor $\vec{b}-\vec{a}$. Die anschließenden Rechnungen sind in beiden Fällen die gleichen.
Für die Länge des Vektors $\vec{a}$ gilt: $|\vec{a}|=\sqrt{a_{1}^{2}+a_{2}^{2}}$. Also gilt auch für die quadrierte Länge: $|\vec{a}|^{2}=a_{1}^{2}+a_{2}^{2}$.
Mithilfe der Längen der drei obigen Vektoren können wir den Satz des Pythagoras anwenden:
Antwort
$$|\vec{a}-\vec{b}|^{2} = |\vec{a}|^{2}+|\vec{b}|^{2}$$
Wir berechnen nun die linke Seite:
Antwort
$|\vec{a}-\vec{b}|^{2} = (a_{1}-b_{1})^{2} + (a_{2}-b_{2})^{2}$
Ausmultiplizieren bzw. binomische Formel anwenden und vereinfachen liefert:
Antwort
$\begin{aligned} (a_{1}-b_{1})^{2} + (a_{2}-b_{2})^{2} &= \left(a_{1}^{2}-2a_{1}b_{1}+b_{2}^{2}\right) + \left(a_{2}^{2}-2a_{2}b_{2}+b_{2}^{2}\right)\\\\ &= a_{1}^{2}+a_{2}^{2}+b_{1}^{2}+b_{2}^{2}-2(a_{1}b_{1}+a_{2}b_{2}) \end{aligned}$
Nun berechnen wir die rechte Seite:
Antwort
$|\vec{a}|^{2}+|\vec{b}|^{2} = a_{1}^{2}+a_{2}^{2}+ b_{1}^{2}+b_{2}^{2}$
Setzen wir beide Seiten in die ursprüngliche Gleichung ein, so ergibt sich:
Antwort
$a_{1}^{2}+a_{2}^{2}+b_{1}^{2}+b_{2}^{2}-2(a_{1}b_{1}+a_{2}b_{2}) = a_{1}^{2}+a_{2}^{2}+ b_{1}^{2}+b_{2}^{2}$
Vereinfachen liefert:
Antwort
$-2(a_{1}b_{1}+a_{2}b_{2}) = 0 \Leftrightarrow a_{1}b_{1}+a_{2}b_{2} = 0$
Zwei Vektoren $\vec{a}$, $\vec{b}$ stehen also genau dann orthogonal zueinander, wenn:
Antwort
$$a_{1}b_{1}+a_{2}b_{2} = 0$$