Osterdatum im Kopf berechnen
HINWEIS: Bitte die Seite ein zweites Mal laden. Die Animationen laden momentan leider noch nicht, wie sie sollen.
# Einleitung
Ostern ist ein beweglicher Feiertag. Das Osterfest scheint von Jahr zu Jahr recht zufällig hin und her zu springen. Zu erklären warum und wie man das Osterdatum im Kopf berechnen kann, ist das Ziel dieses Artikels.
Zunächst werde ich im Theorieteil die historischen, mathematischen und astronomischen (Ostern hat schließlich etwas mit den Mondphasen zu tun) erklären. Anschließend werde ich die Rechenmethode vorstellen, welche zu großen Teilen auf der Osterformel von Carl Friedrich Gauß fußt und abschließend folgen noch ein paar Rechenbeispiele samt Empfehlungen für weiterführende Literatur.
Im Kapitel der Rechenmethode wird die Herkunft der verwendeten Formel zwar nicht explizit erklärt, jedoch finden sich im Theorieteil einige unterstrichene Zahlen. Die Theorie hinter diesen Zahlen liefert eine Idee, warum die Formel, die diese Zahlen enthalten, so sind wie sie sind.
# Theorie
# Sonnen- und Mondkalender
Die Erde bewegt sich in rund 365,242 Tagen einmal um die Sonne — auch tropisches Jahr genannt. Das Kalenderjahr hat jedoch nur 365 Tage und ist damit etwas zu kurz. Aus diesem Grund wurden schon in dem von Julius Caesar eingeführten julianischen Kalender gelegentlich Schalttage eingefügt, um die durchschnittliche Länge des Kalenders näher an den tatsächlichen Wert zu bringen. Jedes vierte Jahr wurde der 29. Februar eingefügt. Damit betrug die durchschnittliche Länge des Kalenderjahres 365,25 Tage, was 365,242 Tagen sehr nahe kommt.
Der Mond durchläuft von Neumond zu Neumond verschiedene Phasen. Ein solcher Durchgang — auch Lunation genannt — dauert durchschnittlich 29,53 Tage. Diese Dauer nennt man synodischer Monat, bzw. für unsere Zwecke einfach Mondmonat. Für die Osterberechnung, für die Mondphasen entscheidend sind, wurde mit der Näherung 29,5 Tage (gerundet 30 Tage) gerechnet. Es fällt auf, dass 12 Mondmonate kürzer sind als 12 Monate, nämlich nur rund 354 Tage lang und damit gut 11 Tage kürzer als ein Kalenderjahr.
Ist also an einem bestimmten Datum Neumond, so ist im darauffolgenden Jahr 11 Kalendertage früher Neumond. Im Kalender gesehen wandert der Mond quasi jedes Jahr um 11 Tage nach vorne (Richtung Jahresbeginn).
Interessanterweise sind 19 Kalenderjahre beinahe genau so lang sind wie 235 Mondmonate.
$$\begin{align*} 19 \cdot 365,25 &= 6939,75 \text{\quad(19 Kalenderjahre)}\\ 235 \cdot 29,53 &= 6939,55 \text{\quad(235 Mondmonate)}\\ \end{align*}$$
Das bedeutet, dass sich die Mondphasen alle 19 Kalenderjahre wieder (mehr oder weniger) genau an derselben Stelle im Kalender befinden.
# Gregorianische Kalenderreform
So genau die Längen von Kalenderjahr und tropischem Jahr sowie von 19 Kalenderjahren und 235 Mondmonaten zusammenliegen, so sind sie doch nicht genau gleich. Und über die Jahrhunderte wurde dies zu einem immer größer werdenden Problem. Da das Kalenderjahr etwas zu lang ist, lief der Kalender im Jahr 1582 dem tatsächlichen Lauf der Sonne um volle 10 Tage hinterher. Auch die berechneten Mondphasen lagen 3 Tage von der tatsächlichen Mondphase entfernt.
Die von Papst Gregor XIII. in diesem Jahre angestoßene Kalenderreform sollte dies beheben. Den entstandenen gregorianische Kalender benutzen wir in dieser Form noch heute. Zur Korrektur des Sonnenjahres wurden einmalig 10 Tage ausgelassen und es werden fortan innerhalb eines Zeitraums von 400 Jahren immer jeweils 3 Schalttage ausgelassen (z. B. sind die Jahre 1700, 1800, 1900 nach der neuen Regel keine Schaltjahre mehr, das Jahr 2000 hingegen bleibt ein Schaltjahr). Zur Korrektur des Mondzyklen setzte man den errechneten Mond einmalig um drei Tage zurück, um fortan den errechneten Mond alle 300 Jahre um einen Tag zurückzusetzen. 1
# Rechengrundlagen
Bei der Berechnung des Osterdatums werden wir ein wenig rechnen müssen, jedoch wird nichts schwierigeres als die Grundrechenarten nötig sein. Im Folgenden werden ein paar Hinweise zur Schreibweise und Tipps zum einfacheren Rechnen gegeben.
# Division mit Rest
Bei der Division mit Rest schreibt man sowohl auf, wie oft eine Zahl in eine andere “passt” und wie viel als Rest übrig bleibt, z. B.:
$100 \div 7 = {\color{blue}{14}} \text{ Rest } {\color{red}{2}}$
Es gibt in der Mathematik zwei verschiedene Schreibweisen um nur das maximal passende Vielfache bzw. nur den Rest zu betrachten:
$\lfloor \frac{100}{7} \rfloor = {\color{blue}{14}}$
$100 \pmod{7} = {\color{red}{2}}$
Die zweite Schreibweise für den Rest wird $\text{modulo}$ ausgesprochen und man kann sich vorstellen, dass man in unserem Beispiel so lange $7$ von der $100$ abzieht, bis man eine positive Zahl erreicht hat, die kleiner als $7$ ist.
Da wir die Division mit Rest für die Zahl $19$ brauchen werden, schauen wir uns diese kurz genauer an. Vielfache von $19$, die man sich merken sollte sind: $19$, $38$, $57$, $76$, $95$. Diese ziehen wir an beliebigen Stellen einer Jahreszahl so lange ab, bis wir eine positive Zahl kleiner als $19$ erreicht haben. Beispiel für das Jahr $2070$:
$$ \begin{matrix} & 2 & 0 & 7 & 0 & & \longrightarrow & & 1 & 7 & 0 & & \longrightarrow & & 1 & 1 & 3 & & \longrightarrow & & 1 & 8 \\\ - & 1 & 9 & & & & & - & & 5 & 7 & & & - & & 9 & 5 & & & & & \\\ \end{matrix} $$
Wenn man $95$ abzieht, kann man sich stattdessen auch denken, dass man $100$ abzieht und $5$ addiert. Also $1$ weniger und zwei Stellen rechts davon $5$ mehr. So wurde aus $113$ die $18$. Man hätte auch die $170$ zu $75$ verändern können:
$$ \begin{matrix} & 2 & 0 & 7 & 0 & & \longrightarrow & & 1 & 7 & 0 & & \longrightarrow & & & 7 & 5 & & \longrightarrow & & 1 & 8 \\\ - & 1 & 9 & & & & & - & & 9 & 5 & & & - & & 5 & 7 & & & & & \\\ \end{matrix} $$
Viele Wege führen zum Rest ;)
# Multiplikation mit 11
Die Multiplikation mit 11 ist für Zahlen zwischen 1 und 18 besonders einfach.
Einstellige Zahlen werden einfach verdoppelt:
$11 \cdot 4 = 44$
$11 \cdot 7 = 77$
etc.
Bei zweistelligen Zahlen bleiben die beiden Ziffern links und rechts stehen und zwischen diese schreibt man die Summe der beiden Ziffern:
$11 \cdot 13 = 1(1+3)3 = 143$
$11 \cdot 15 = 1(1+5)5 = 165$
$11 \cdot 17 = 1(1+7)7 = 187$
etc.
# Die Wochentage auf der Hand
Mithilfe des Daumens können wir wie folgt die verschiedenen Wochentage darstellen:
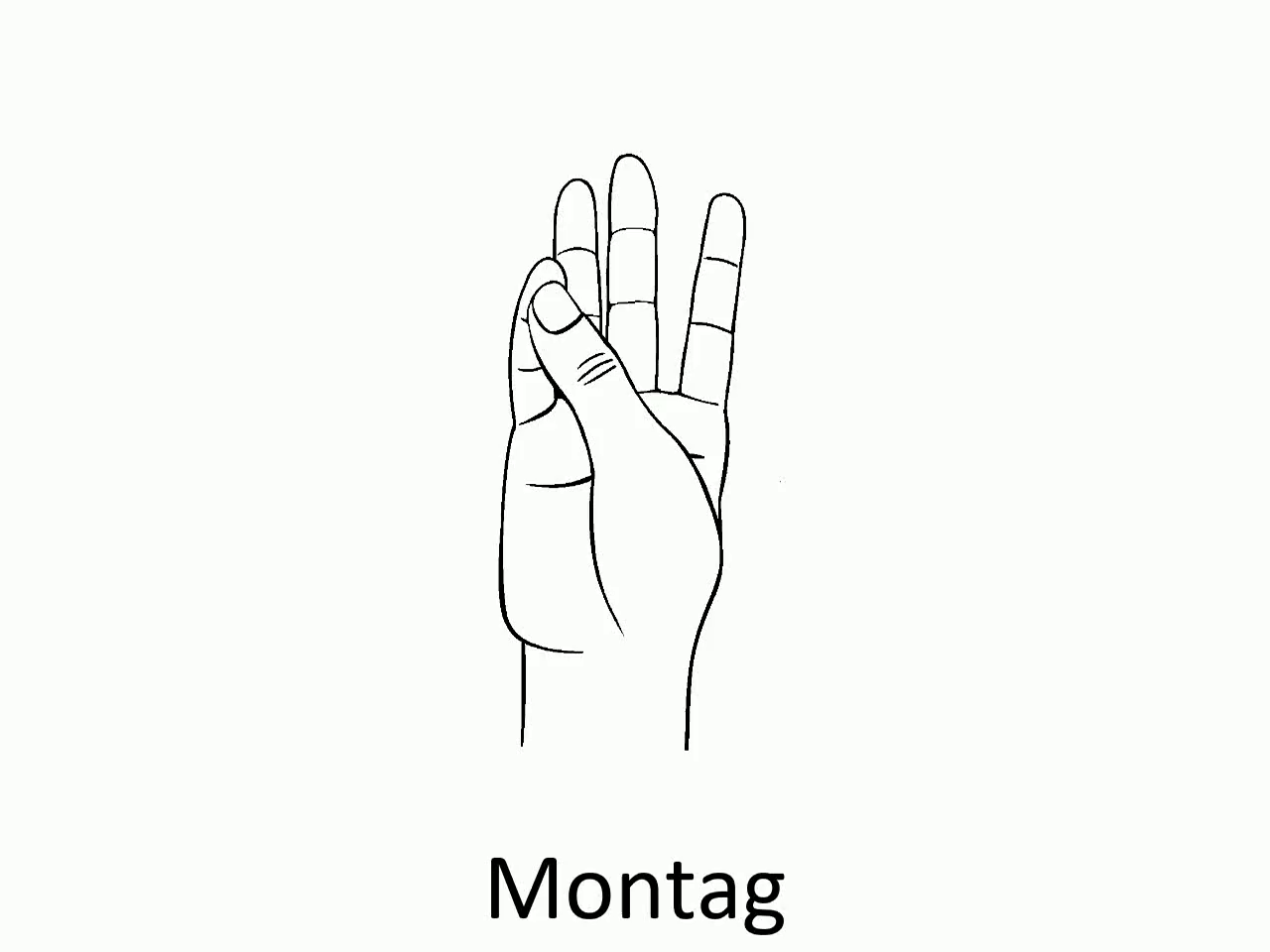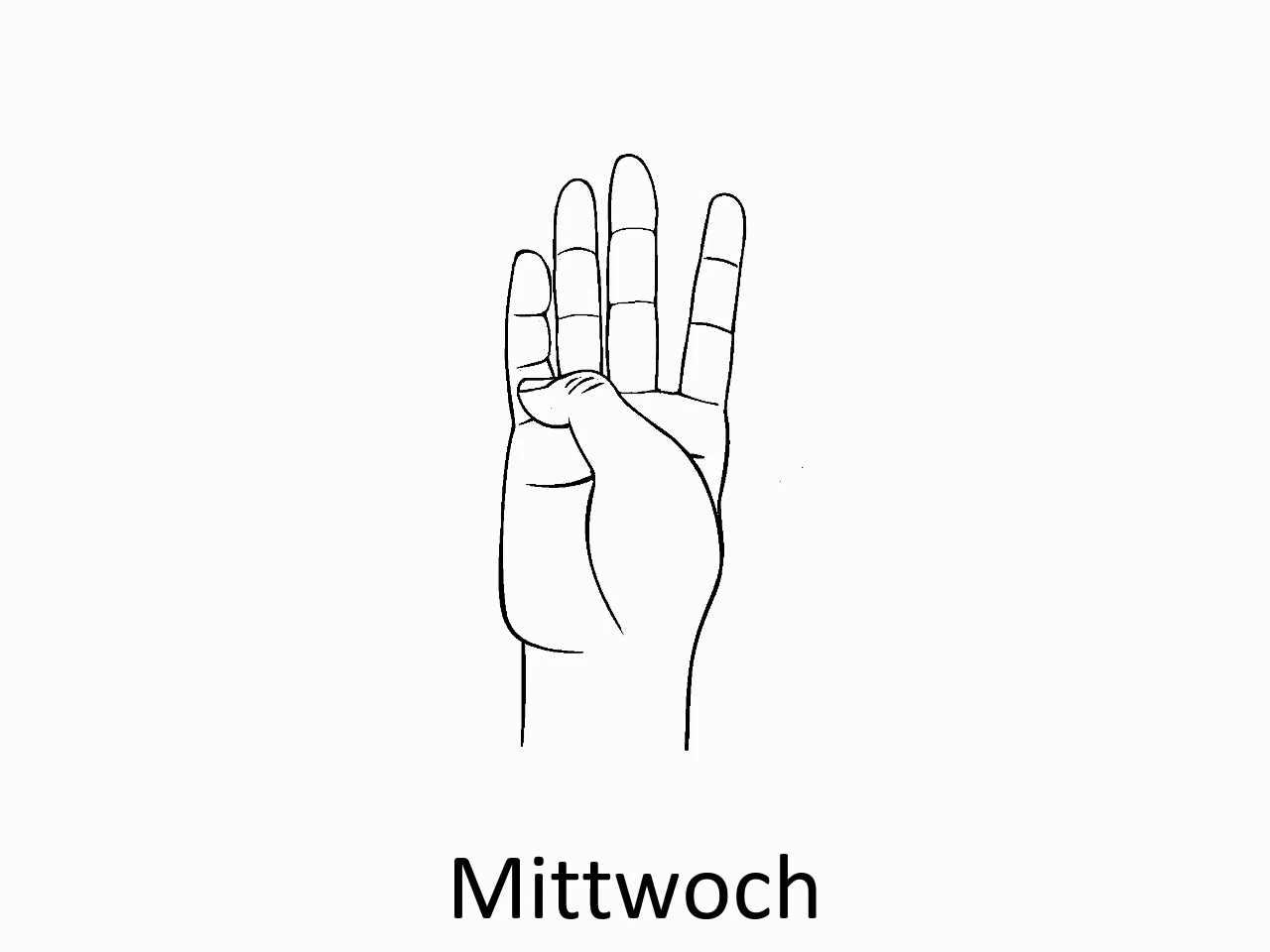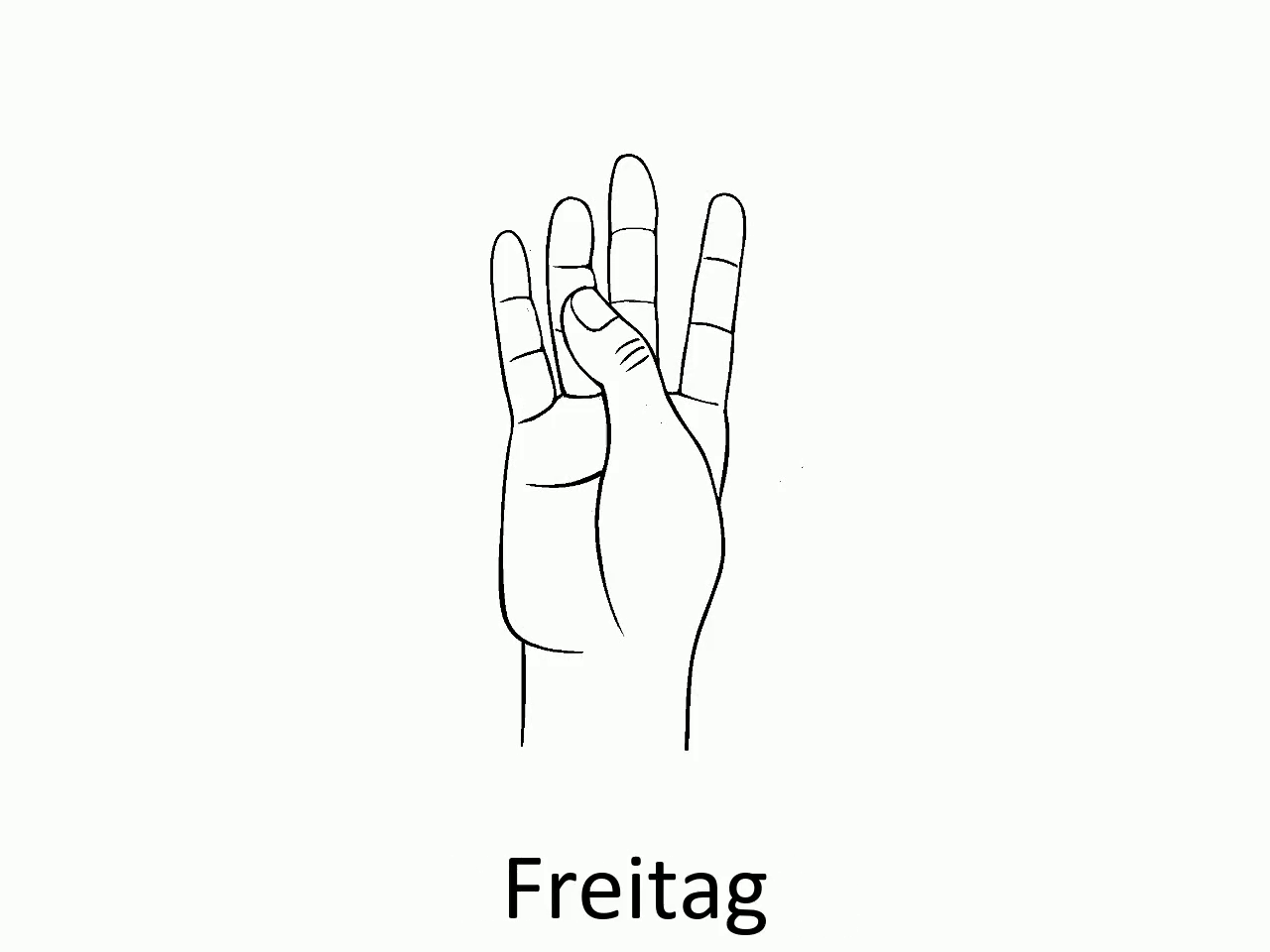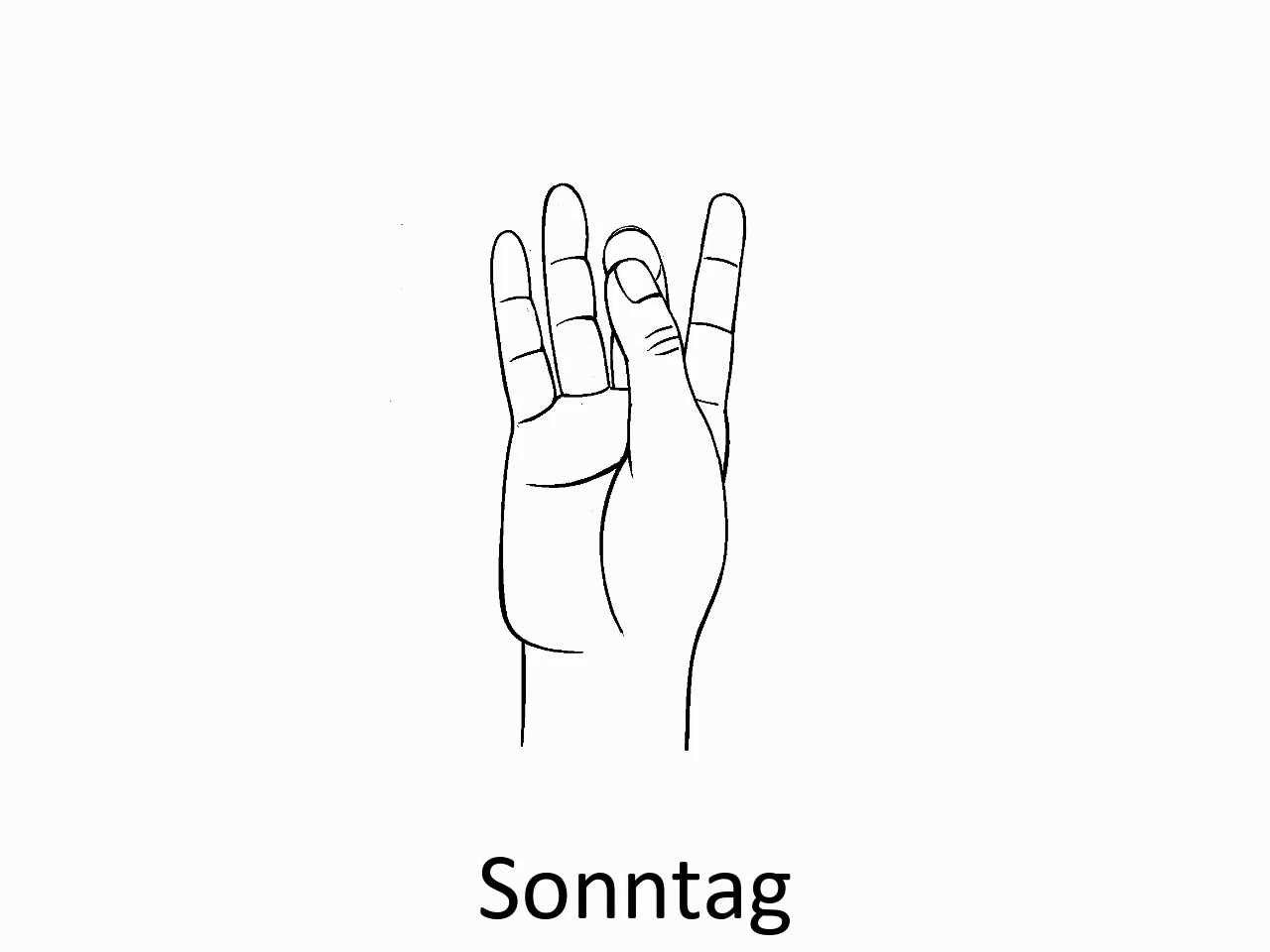
Ist der aktuell mit dem Daumen festgehaltene Tag z. B. ein Donnerstag, dann liegt der Daumen auf dem oberen Knöchel des Ringfingers. Will man den Wochentag 4 Tage später wissen, so geht man mit dem Daumen vier Knöchel weiter und landet beim Sonntag.
Wenn wir mehr als 7 Tage vorwärts gehen müssen, dann können wir Vielfache von 7 abziehen — nach 7 Tagen kommen wir nämlich wieder am selben Wochentag an. Wenn wir also z. B. 18 Tage vorwärts gehen müssen, dann ist das dasselbe, als wenn wir 11 Tage vorwärts gehen. Das ist wiederum dasselbe, als wenn wir 4 Tage vorwärts gehen. Wir müssen also nur $18 \pmod{7} = 4$ Tage vorwärts gehen.
Müssten wir 100 Tage vorwärts gehen, dann wäre das wie oben gesehen dasselbe wie $100 \pmod{7} = 2$ Tage.
# Osterberechnung
# Definition Osterdatum
Die Bestimmung des Osterdatums ist historisch sehr turbulent und wurde im 1. Konzil von Nicäa im Jahr 325 n. Chr. zum ersten Mal einheitlich definiert:
Ostern fällt auf den ersten Sonntag nach dem Tag des ersten Vollmondes nach Frühlingsbeginn. 2
Um also das Osterdatum für ein Jahr berechnen zu können, müssen wir zunächst herausfinden, an welchem Tag der Frühling beginnt. Anschließend müssen wir bestimmen, an welchem Tag der nächstfolgende Vollmond stattfindet und zum Schluss den darauffolgenden Sonntag berechnen.
Wichtig hierbei ist, dass es sich hierbei nicht um die tatsächlichen astronomischen Zeitpunkte von Frühlingsbeginn und Vollmond handelt. Als Frühlingsbeginn wurde fix der 21. März gewählt — der tatsächliche Frühlingsbeginn ist teilweise auch 1 bis 2 Tage früher. Als Mond wird nicht der echte Himmelskörper zurate gezogen, sondern der eben beschriebene errechnete Mond.
# Schritt 1 - Wochentag des Frühlingsbeginns bestimmen
Das Datum des Frühlingsbeginns für die Osterberechnung ist der 21. März. Es bleibt also nur noch den Wochentag dieses Tages für ein bestimmtes Jahr herauszufinden.
Hier bedienen wir uns eines Verfahrens, das ich im Rahmen der Doomsday-Methode entwickelt habe. Mit der Doomsday-Methode kann man den Wochentag eines beliebigen Datums bestimmen. Wen die Hintergründe interessieren, warum das gezeigte Verfahren den Wochentag des Frühlingsbeginns bestimmen kann, der liest am besten den Artikel zur Doomsday-Methode. So viel sei gesagt, der 21. März ist zufälligerweise genau ein Doomsday ;)
Im Folgenden werde ich lediglich das Verfahren ohne Erklärung geben.
Wir denken uns auf unser Hand ein bei Dienstag beginnendes Häkchen ✔️.
Wir gehen zunächst wie folgt vor:
Wir denken uns die ersten beiden Ziffern der gewünschten Jahreszahl und setzen den Daumen auf Dienstag.
In 1er-Schritten entlang des Häkchens gehen, bis zum nächsten Vielfachen von 4.
Dort bleibt der Daumen und wir denken uns die letzten beiden Ziffern der gewünschten Jahreszahl.
Bei 0 beginnend nähern wir uns nun dieser Zahl so weit es geht in 12er-Schritten und gehen pro 12er-Schritt mit dem Daumen um einen Knöchel vor.
Wir schauen wie viel jetzt noch zur gewünschten Zahl fehlt. Bei der 0 beginnend gehen wir so viele Male 1 Knöchel vorwärts. Bei der 4 und 8 jedoch gehen wir um 2 Knöchel vorwärts.
Der Wochentag auf dem der Daumen jetzt liegt, ist der Wochentag des 21.03.
# Beispiel 2045
# Beispiel 1965
# Beispiel 1789
# Schritt 2 - Wochentag und Datum des Vollmondes berechnen
Der schwierigste Schritt ist die Berechnung des Wochentags und des Datums des Vollmondes. Diese erfolgt in 3 Schritten:
- Abstand des Vollmondes vom 21.03. berechnen
- Wochentag des Vollmondes bestimmen
- Datum des Vollmondes bestimmen
# 1. Abstand des Vollmondes vom 21.03. berechnen
Wir führen hierfür zunächst zwei Schreibweisen ein:
$J$: Jahreszahl
$H$: vorderen beiden Ziffern des Jahres
Für das Jahr $2045$ wäre also $J = 2045$ und $H = 20$.
Für die Berechnung des Vollmondes müssen wir ein paar Zwischenergebnisse ausrechnen und diese jeweils weiterverarbeiten. Die Zwischenergebnisse $a$ und $b$ braucht man, um $c$ auszurechnen.
Bei der Berechnung der Variablen $a$ und $b$ helfen uns unsere Rechentipps aus obigem Kapitel.
$a = J \pmod{19}$
$b = 11a \pmod{30}$
$c = D - b \pmod{30}$
Sollte bei der Berechnung von $c$ ein negatives Ergebnis auftauchen, addiert man einfach einmal $30$ damit man wieder eine positive Zahl erhält.
Die Variable $D$ ist für ein ganzes Jahrhundert immer gleich, sodass man sich dieses auch einfach merken kann. Für die Jahrhunderte, die an $1900$, $2000$ und $2100$ beginnen ist der Wert für $D = 24$. Für andere Jahrhunderte berechnet man $D$ wie folgt:
$D = H - \lfloor \frac{H}{3} \rfloor - \lfloor \frac{H}{4} \rfloor +15$ 3
Der Wert für $D$ steigt also jedes Jahrhundert um $1$. Wenn das Jahrhundert bzw. die ersten beiden Ziffern des Jahres ($H$) durch $3$ oder $4$ teilbar sind, dann bleibt der Wert, wie er ist. Ist $H$ sogar durch $12$ teilbar, also sowohl durch $3$ und $4$ teilbar, dann verringert sich der Wert von $D$ sogar um $1$.
Hier ein paar Werte für $D$:
| $H$ | $D$ |
|---|---|
| $15$ | $22$ |
| $16$ | $22$ |
| $17$ | $23$ |
| $18$ | $23$ |
| $19$ | $24$ |
| $20$ | $24$ |
| $21$ | $24$ |
| $22$ | $25$ |
| $23$ | $26$ |
| $24$ | $25$ |
| $25$ | $26$ |
Vollmond ist dann $c$ Tage nach dem 21.03.
# 2. Wochentag des Vollmondes bestimmen
Wir gehen nun also mit dem Daumen $c$ Tage nach vorne, um den Wochentag des Vollmondes zu erhalten. Hierbei kann man wie im Theorieteil gesehen auch Vielfache von $7$ abziehen. Wenn ich z. B. $23$ Tage nach vorne gehe, dann kann ich auch einfach nur $2$ Tage nach vorne gehen, da $23 \pmod{7} = 2$.
# 3. Datum des Vollmondes bestimmen
Um das Datum des Vollmondes zu bestimmen, muss man schlicht zum 21.03. $c$ Tage hinzuzählen. Wir können uns allerdings einen Umstand zunutze machen. $11$ Tage nach dem 21.03. ist der 1. April. Wenn also $c>10$ ist, dann müssen wir von $c$ einfach $10$ abziehen und erhalten den Tag des Datums im April.
Wenn $c \leq 10$, dann ist der Vollmond am ($21 + c$). März.
Wenn $c > 10$, dann ist der Vollmond am ($c-10)$. April.
Beispiele:
Ist $c = 4$, dann ist der Vollmond am 25.03.
Ist $c =10$, dann ist der Vollmond am 31.03.
Ist $c = 13$, dann ist der Vollmond am 03.04.
Ist $c = 21$, dann ist der Vollmond am 11.04.
# Schritt 3 - Datum des folgenden Sonntags bestimmen
Wir kennen nun also den Wochentag und das Datum des ersten Frühlingsvollmondes. Den darauffolgenden Sonntag zu finden ist ein Leichtes. Wir gehen schlicht mit dem Daumen zum nächsten Sonntag und zählen dabei beim Datum pro Knöchel, den wir voranschreiten, 1 Tag weiter. Ist der Vollmond an einem Sonntag, so gehen wir zum nächsten Sonntag.
Das war’s :)
# Zwei Ausnahmen
Keine Regel ohne Ausnahme, so auch bei der Osterberechnung. Vor der gregorianischen Kalenderreform war der 25.04. der letztmögliche Ostertermin. Dies sollte auch nach der Reform so bleiben, allerdings konnte es nun sein, dass Ostern nach den Berechnungsregeln in seltenen Fällen auch am 26.04. stattfinden hätte müssen. Dies sollte auf jeden Fall verhindert werden. Der Grund der zweiten Ausnahmeregel wird an dieser Stelle nicht erklärt. Hierfür wird auf eine externe Quelle verwiesen. Die Ausnahmeregeln lauten:
Ausnahmeregel 1: Fällt Ostern laut Berechnung auf den 26.04., so wird es stattdessen eine Woche nach hinten verschoben auf den 19.04.
Ausnahmeregel 2: Fällt Ostern laut Berechnung auf den 25.04. UND ist der Vollmond an einem Sonntag UND ist $a > 10$, dann wird es stattdessen eine Woche nach hinten verschoben auf den 18.04. (Ist auch nur eine der 3 Bedingungen nicht erfüllt, so bleibt es bei dem errechneten Osterdatum.)
# Beispiele
# Jahr 2045
# Schritt 1
# Schritt 2
$a$ berechnen
$$ \begin{matrix} & 2 & 0 & 4 & 5 & & \longrightarrow & & 1 & 4 & 5 & & \longrightarrow & & 1 & 0 & 7 & & \longrightarrow & & 1 & 2 \\\ - & 1 & 9 & & & & & - & & 3 & 8 & & & - & & 9 & 5 & & & & & \\\ \end{matrix} $$
$b$ berechnen
$$\begin{align*} b &= 1(1+2)2 \pmod{30}\\ &= 132 \pmod{30}\\ &= 12 \end{align*}$$
$c$ berechnen
$$\begin{align*} c &= 24 - 12 \pmod{30}\\ &= 12 \end{align*}$$
Vollmond ist also 12 Tage nach dem 21.03., also am 02.04.
Der 21.03. ist wie in Schritt 1 gesehen ein Dienstag. 12 Tage später ist also ein Sonntag, da man von Dienstag $12 \pmod{7} = 5$ Tage vorwärts gehen muss.
Der Vollmond findet also am Sonntag, den 02.04. statt.
# Schritt 3
Der folgende Sonntag ist 7 Tage später, also am 09.04.
Ostersonntag 2045 ist also der 09.04.
# Jahr 1801
# Schritt 1
# Schritt 2
$a$ berechnen
$$ \begin{matrix} & 1 & 8 & 0 & 1 & & \longrightarrow & & 1 & 0 & 4 & 1 & & \longrightarrow & & & 9 & 1 & & \longrightarrow & & 1 & 5 \\\ - & & 7 & 9 & & & & - & & 9 & 5 & & & & - & & 7 & 6 & & & & & \\\ \end{matrix} $$
$b$ berechnen
$$\begin{align*} b &= 1(1+5)5 \pmod{30}\\ &= 165 \pmod{30}\\ &= 15 \end{align*}$$
$c$ berechnen
$$\begin{align*} c &= 23 - 15 \pmod{30}\\ &= 8 \end{align*}$$
Vollmond ist also 8 Tage nach dem 21.03., also am 29.03.
Der 21.03. ist wie in Schritt 1 gesehen ein Samstag. 8 Tage später ist also ein Sonntag, da man von Samstag $8 \pmod{7} = 1$ Tag vorwärts gehen muss.
Der Vollmond findet also am Sonntag, den 29.03. statt.
# Schritt 3
Der folgende Sonntag ist 7 Tage später, also am 05.04.
Ostersonntag 1801 ist also der 05.04.
# Jahr 1981
# Schritt 1
# Schritt 2
$a$ berechnen
$$ \begin{matrix} & 1 & 9 & 8 & 1 & & \longrightarrow & & & 8 & 1 & & \longrightarrow & & 5 \\\ - & 1 & 9 & & & & & - & & 7 & 6 & & & & \\\ \end{matrix} $$
$b$ berechnen
$$\begin{align*} b &= 55 \pmod{30}\\ &= 25 \\ \end{align*}$$
$c$ berechnen
$$\begin{align*} c &= 24 - 25 \pmod{30}\\ &= -1 \pmod{30}\\ &= 29 \end{align*}$$
Vollmond ist also 29 Tage nach dem 21.03., also am 19.04.
Der 21.03. ist wie in Schritt 1 gesehen ein Samstag. 29 Tage später ist also ein Sonntag, da man von Samstag $29 \pmod{7} = 1$ Tag vorwärts gehen muss.
Der Vollmond findet also am Sonntag, den 19.04. statt.
# Schritt 3
Der folgende Sonntag ist 7 Tage später, also am 26.04.
Ausnahmeregel 1: Ostern fällt zurück auf den 19.04.
Ostersonntag 1981 ist also der 19.04.
# Jahr 2106
# Schritt 1
# Schritt 2
$a$ berechnen
$$ \begin{matrix} & 2 & 1 & 0 & 6 & & \longrightarrow & & 2 & 0 & 6 & & \longrightarrow & & 1 & 6 \\\ - & 1 & 9 & & & & & - & 1 & 9 & & & & & & \\\ \end{matrix} $$
$b$ berechnen
$$\begin{align*} b &= 1(1+6)6 \pmod{30}\\ &= 176 \pmod{30}\\ &= 26 \end{align*}$$
$c$ berechnen
$$\begin{align*} c &= 24 - 26 \pmod{30}\\ &= -2 \pmod{30}\\ &= 28 \end{align*}$$
Vollmond ist also 28 Tage nach dem 21.03., also am 18.04.
Der 21.03. ist wie in Schritt 1 gesehen ein Sonntag. 28 Tage später ist also ein Sonntag, da man von Samstag $28 \pmod{7} = 0$ Tage vorwärts gehen muss.
Der Vollmond findet also am Sonntag, den 18.04. statt.
# Schritt 3
Der folgende Sonntag ist 7 Tage später, also am 25.04.
Ausnahmeregel 2: Ostern fällt laut Berechnung auf den 25.04. UND der Vollmond ist an einem Sonntag UND $a > 10$. Ostern fällt also zurück auf den 18.04.
Ostersonntag 2106 ist also der 18.04.
# Weiterführende Literatur
# Internet
- Youtube - Easter, Passover, and Astronomy: Why the different dates? Explained!
- nabkal.de - Webseite mit umfassenden Informationen und Rechnern zu Kalender- und Osterthemen
# Bücher
- Walther Jacobsthal (1917) - Mondphasen, Osterrechnung und Ewiger Kalender
- Michael E. Klews (2008) - Die Herleitung der Osterformeln von Gauß, Butcher & Jones, Meeus sowie Knuth aus dem computus paschalis
Das stimmt nicht ganz. Genau genommen sollte der errechnete Mond ab dem Jahr 1800 siebenmal jeweils alle 300 Jahre um einen Tag zurückgesetzt werden und danach einmal nach 400 Jahren. Dieser 2500 Jahre dauernde Zyklus wiederholt sich anschließend immer wieder. Unsere vereinfachte Regel von oben, weicht als von der tatsächlichen erst ab dem Jahr 4200 ab. Bis dahin soll diese Näherung genügen. ↩︎
Ist der Vollmond an einem Sonntag, so findet Ostern am darauffolgenden Sonntag statt. (siehe auch das Unterkapitel “Zwei Ausnahmen”) ↩︎
Die 3 und die 4 in den Rechnungen kommen durch die Korrekturen in der gregorianischen Kalenderreform alle 300 bzw. 400 Jahre. $\lfloor \frac{H}{3} \rfloor$ ist die Korrektur für den Mond und $\lfloor \frac{H}{4} \rfloor$ für die Sonne. ↩︎