Pythagoras mit dem Skalarprodukt
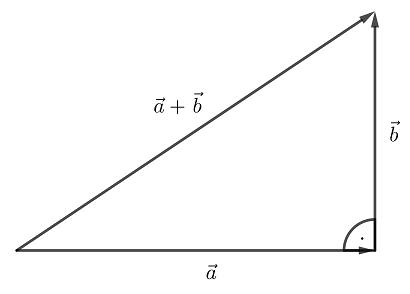
$$\begin{aligned}|\vec{a}+\vec{b}|^2&=(\vec{a}+\vec{b})\cdot(\vec{a}+\vec{b})\\&=\vec{a}\cdot\vec{a}+\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{a}+\vec{b}\cdot\vec{b}\qquad&&\text{(das Distributivgesetz gilt für das Skalarprodukt *)}\\&=\vec{a}\cdot\vec{a}+\vec{b}\cdot\vec{b}&&\text{(da } \vec{a}\text{ und } \vec{b} \text{ orthogonal sind, gilt: } \vec{a}\cdot\vec{b}=0 \text{ und } \vec{b}\cdot\vec{a}=0)\\&=|\vec{a}|^2+|\vec{b}|^2\end{aligned}$$
* Warum das Distributivgesetz beim Skalarprodukt gilt.