Rätsel Kürzester Weg zwischen zwei Punkten
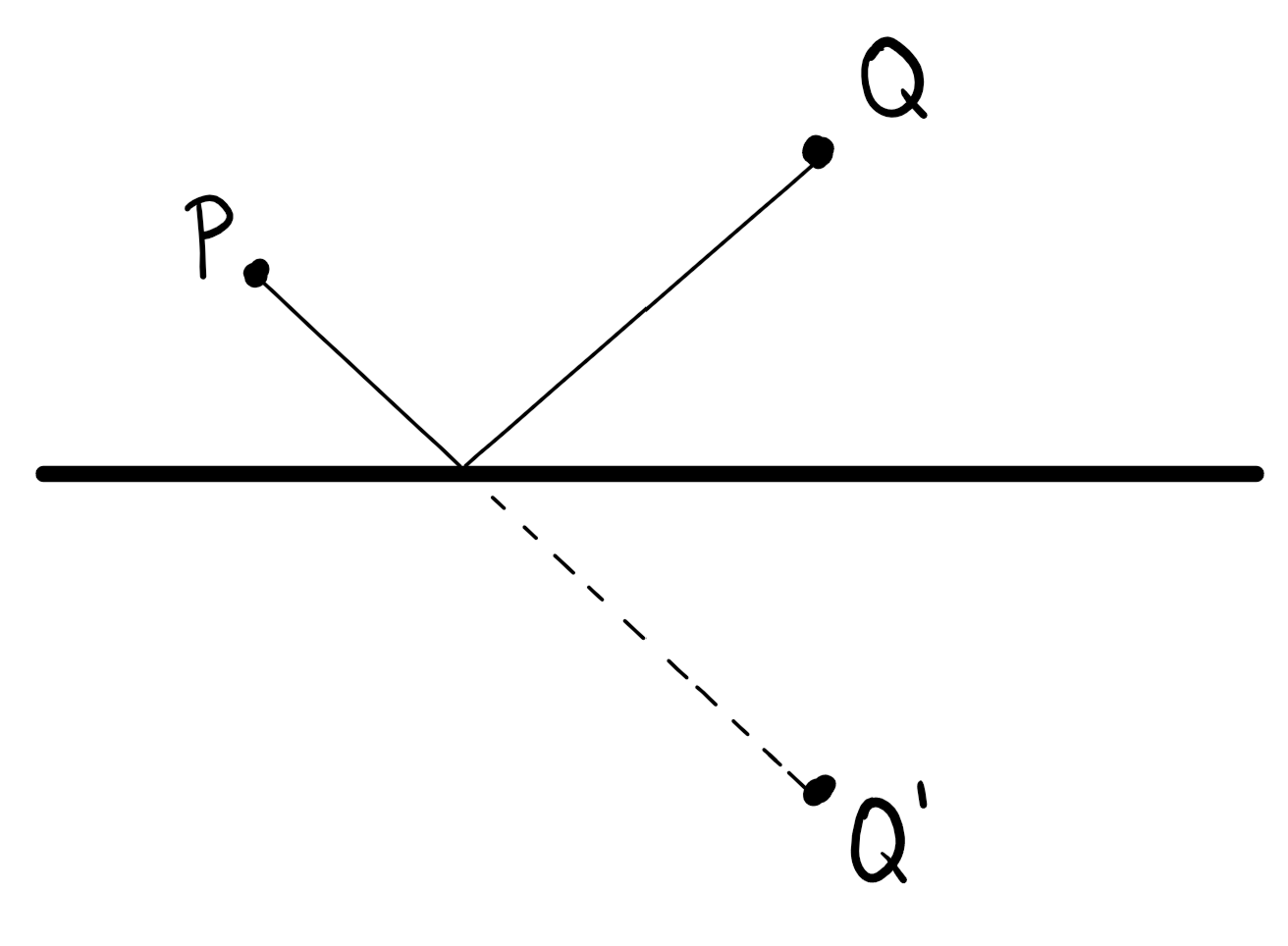
Wie findet man den kürzesten Weg zwischen zwei Punkten, wenn dieser die darunterliegende Gerade berühren muss?

Tipps
- Was wäre die Lösung, wenn man die Gerade nicht berühren müsste?
- Was wäre die Lösung, wenn ein Punkt oberhalb und ein Punkt unterhalb der Geraden liegen würde?
Lösung
Spiegelt man den Punkt $Q$ an der Geraden, so erhalten wir einen Punkt $Q’$ auf der anderen Seite der Geraden.
Aufgrund der Symmetrie ist jede Linie, die wir von einem beliebigen Punkt auf der Geraden zum Punkt $Q$ ziehen, genauso lang wie von dem gleichen Punkt auf der Geraden zum gespiegelten Punkt $Q’$.
Der kürzeste Weg von $P$ nach $Q$, der die Gerade berührt, ist derjenige, der gespiegelt genau geradlinig verläuft. Ziehen wir also eine Strecke von $P$ nach $Q’$ und reflektieren den Teil unterhalb der Geraden nach oben, so erhalten wir den gesuchten kürzesten Weg zwischen $P$ und $Q$, der die Gerade berührt.
Erweiterung
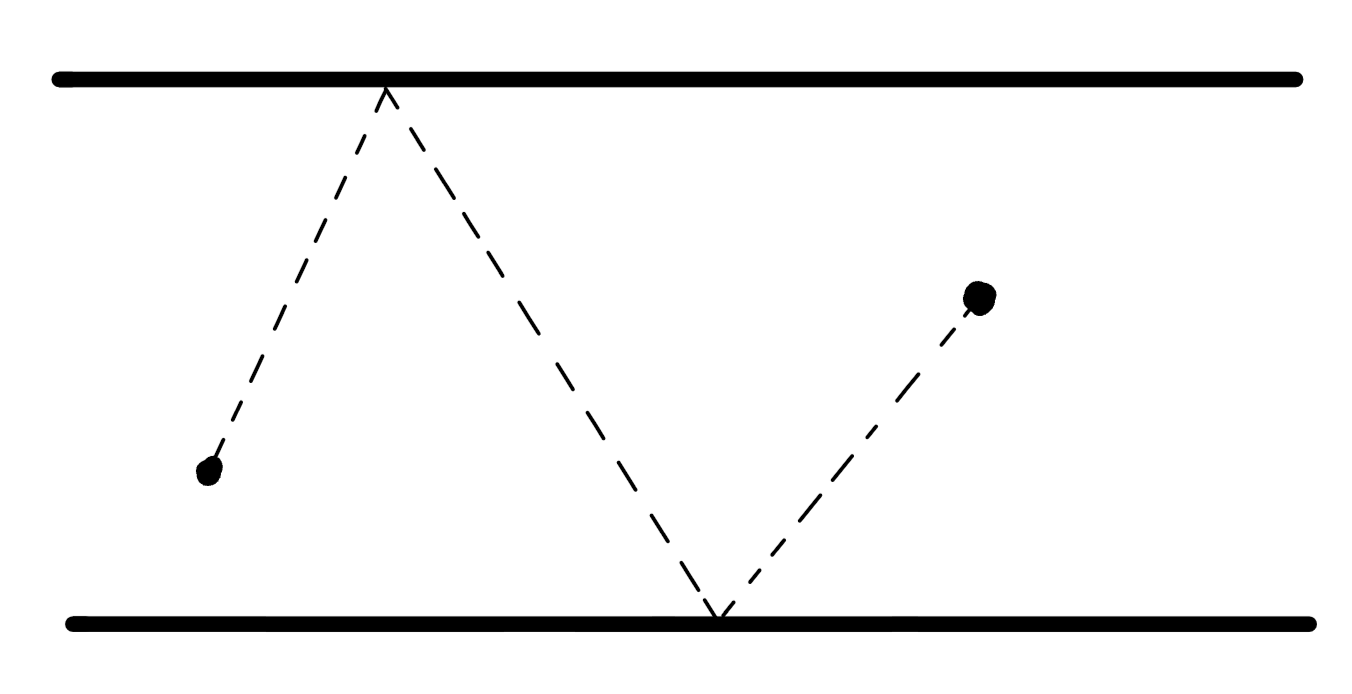
Nehmen wir an, die beiden Punkte liegen zwischen zwei Geraden. Wie findet man den kürzesten Weg zwischen beiden Punkten, der beide Geraden berührt?
Quelle: Paul Lockhart - Measurement (ISBN: 9780674284388)