Zusammenhang Integral und Flächeninhalt
# Fachliche und geschichtliche Einordnung
Auch wenn die folgenden Überlegungen nicht dem heutigen Maßstab der mathematischen Strenge entsprechen, so geben sie doch ein intuitives Verständnis dafür, wie Integrale und der Flächeninhalt unter Graphen zusammenhängen.
Bei diesen intuitiven Überlegungen wird mit unendlich kleinen Größen $\mathrm{d}f$ und $\mathrm{d}x$ gearbeitet, mit welchen in der Entstehungsphase der Integral- und Differentialrechnung im 17. Jahrhundert (damals aufgrund dieser Größen noch Infinitesimalrechnung genannt) trotz ihrer begrifflichen Schwammigkeit recht unbedarft gerechnet wurde. Deren Verwendung lässt sich auch in den von Leibniz eingeführten Schreibweisen, welche noch heute benutzt werden, gut erkennen.
Das Rechnen mit unendlich kleinen Größen wurde erst in den 1960ern von Abraham Robinson auf ein mathematisch sicheres Fundament gestellt. Dieser konnte mithilfe der hyperreellen Zahlen solche unendlich kleinen (sowie unendlich große) Zahlen sauber definieren und mit deren Hilfe die sogenannte Nichtstandardanalysis begründen. Dies erklärt auch, warum Leibniz und Newton mit ihren intuitiven, jedoch schwammigen Vorgehensweisen zu richtigen Ergebnissen kommen konnten. Im Kern waren ihre Überlegungen korrekt, allerdings nur nicht hinreichend präzisiert.
Als intuitives Mittel sind diese Überlegungen jedoch gerade wegen ihrer suggestiven Art, die Teils an einfache Bruchrechnung erinnern lässt, sowie ihrer bildlichen Verständlichkeit gerade für Lernende der Analysis gut geeignet, um die Integral- und Differentialrechnung zu begreifen.
# Funktionsgraph und Ableitungsgraph
Im Folgenden werden die zwei graphischen Interpretationen des Integrals an einem Funktionsgraphen bzw. an dessen Ableitungsgraphen dargestellt. Exemplarisch dienen hierzu die Graphen der Funktionen $f(x)=x^{2}$ und $f’(x)=2x$.
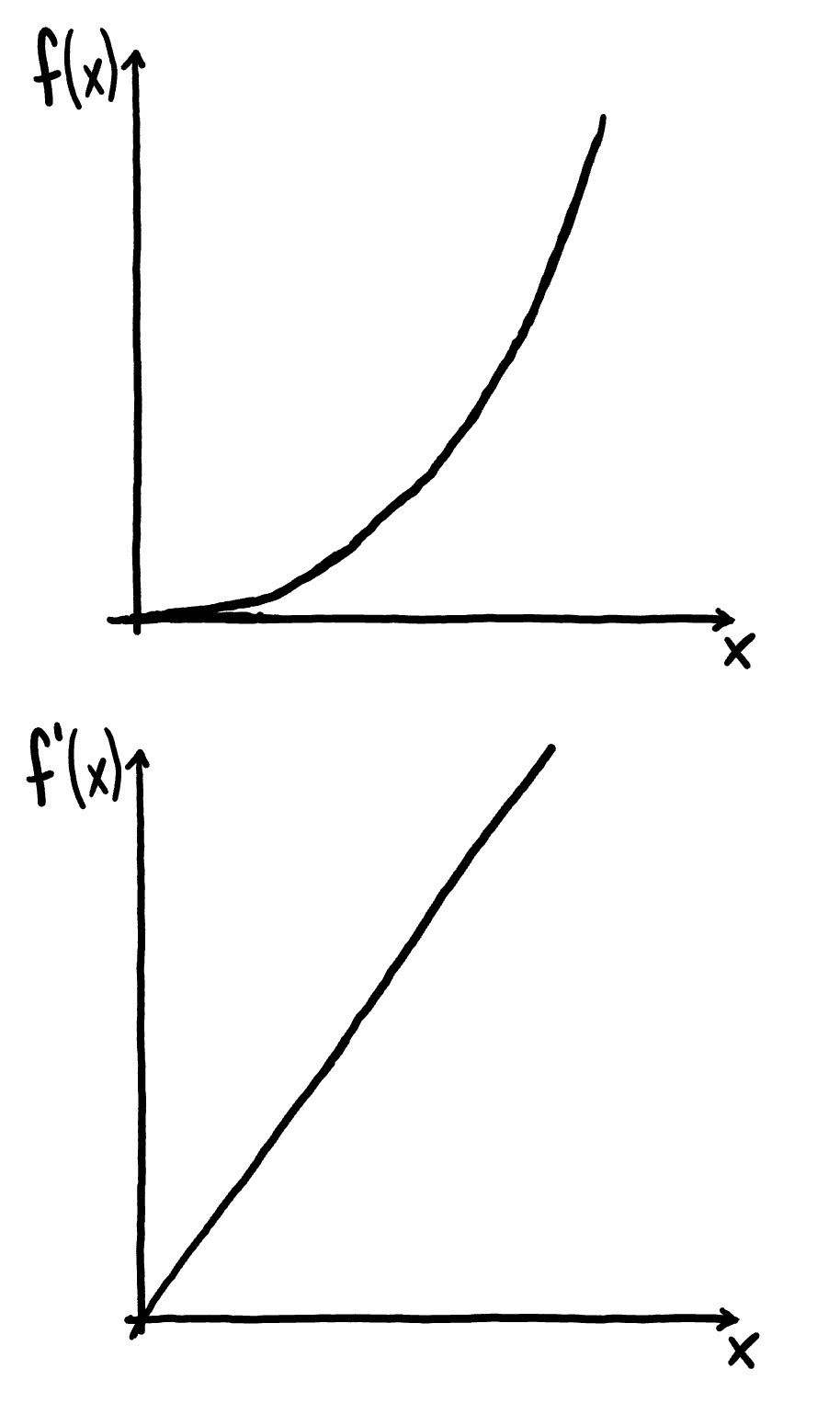
# Integral am Funktionsgraphen
Mithilfe der Steigungen eines Graphen lässt sich der ursprüngliche Graph rekonstruieren (genauer bereits hier behandelt).
Der Funktionswert $f(x)$ an einer Stelle $x$ lässt sich demnach bestimmen, indem man alle infinitesimalen Veränderungen des Funktionswerts $\mathrm{d}f$ aufsummiert. In den folgenden Abbildungen sind diese zur Veranschaulichung mit endlichen Längen dargestellt und nähern den eigentlichen Verlauf von $f(x)$ lediglich an. Wären die Steigungsdreiecke jedoch unendlich klein, so würden die den Verlauf von $f$ genau beschreiben.
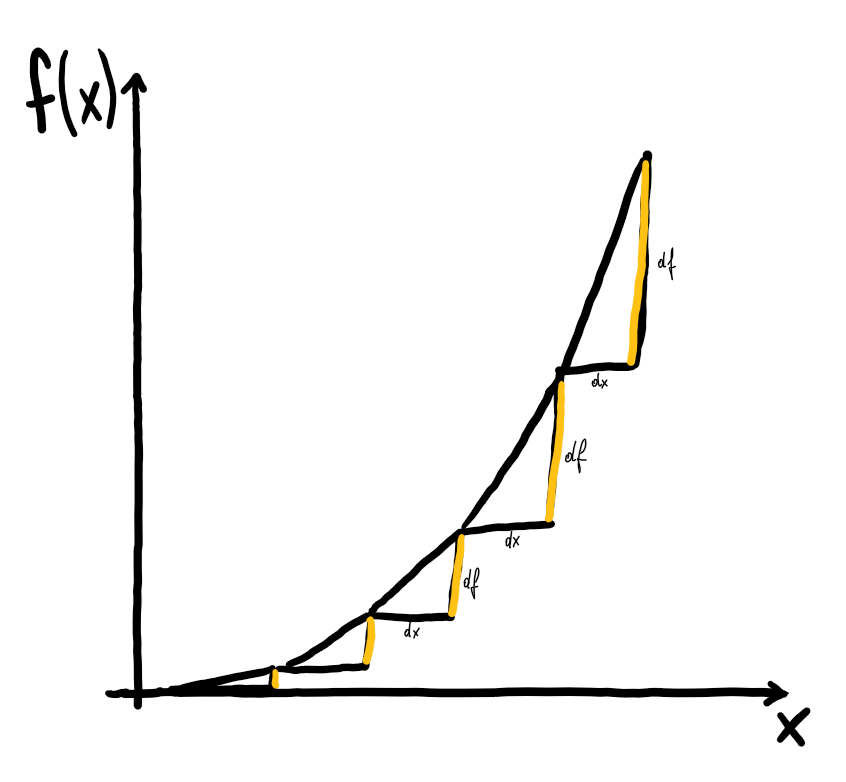
Beim Aufsummieren unendlich kleiner Größen verwendet man ein langgezogenes S, welches für das Wort summa steht. Rechnerisch ausgedrückt besagt obiges Bild demnach:
$$f(x) = \int \mathrm{d}f$$
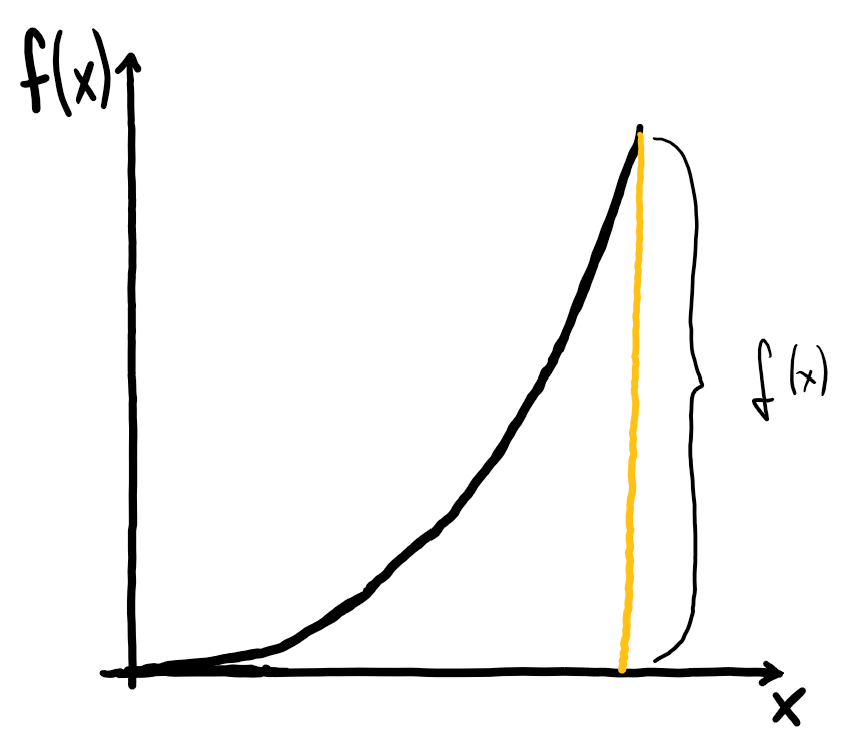
Das Integral rekonstruiert aus den Steigungen eines Funktionsgraphen den ursprünglichen Funktionswert.
Die Ableitung $f’(x)$ schreibt sich in Leibniz-Schreibweise $\frac{\mathrm{d}f}{\mathrm{d}x}$. Dieser Quotient beschreibt die Steigung des unendlich kleinen Steigungsdreiecks.
Da $\frac{\mathrm{d}f}{\mathrm{d}x}=2x \Rightarrow \mathrm{d}f = 2x~\mathrm{d}x$ ergibt sich in unserem Beispiel:
$$f(x)=\int 2x~\mathrm{d}x$$
# Integral am Ableitungsgraphen
Das Integral hat auch eine schöne graphische Bedeutung am Ableitungsgraphen.
Nehmen wir die obige Gleichung für das Integral und “erweitern” mit $\mathrm{d}x$, so erhalten wir:
$$ \begin{align*} f(x) &= \int \mathrm{d}f\\ &= \int \frac{\mathrm{d}f}{\mathrm{d}x} \cdot \mathrm{d}x\\ &= \int f’(x) \cdot \mathrm{d}x \end{align*} $$
Wir summieren also unendlich viele $f’(x) \cdot \mathrm{d}x$ auf. Graphisch entspricht das dem Flächeninhalt von feinen Rechtecken mit der Breite $\mathrm{d}x$ und der Höhe $f’(x)$.
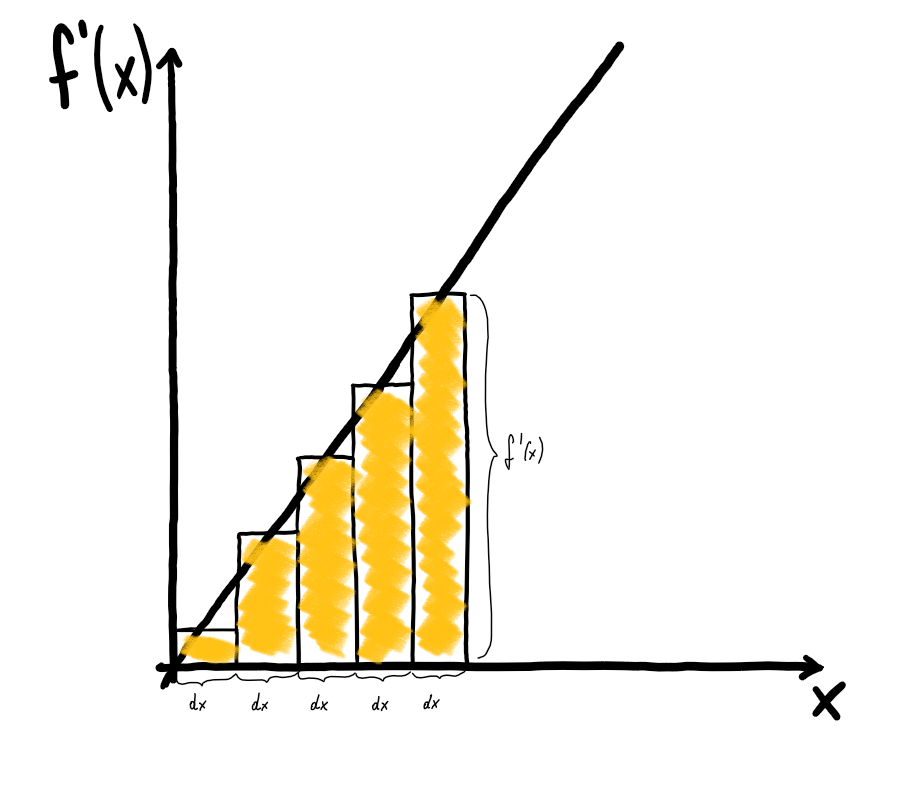
Je feiner die Rechtecke sind, desto genauer wird die Fläche unter dem Ableitungsgraphen $f’(x)$ angenähert. Sind sie unendlich fein, so wird die Fläche genau beschrieben.
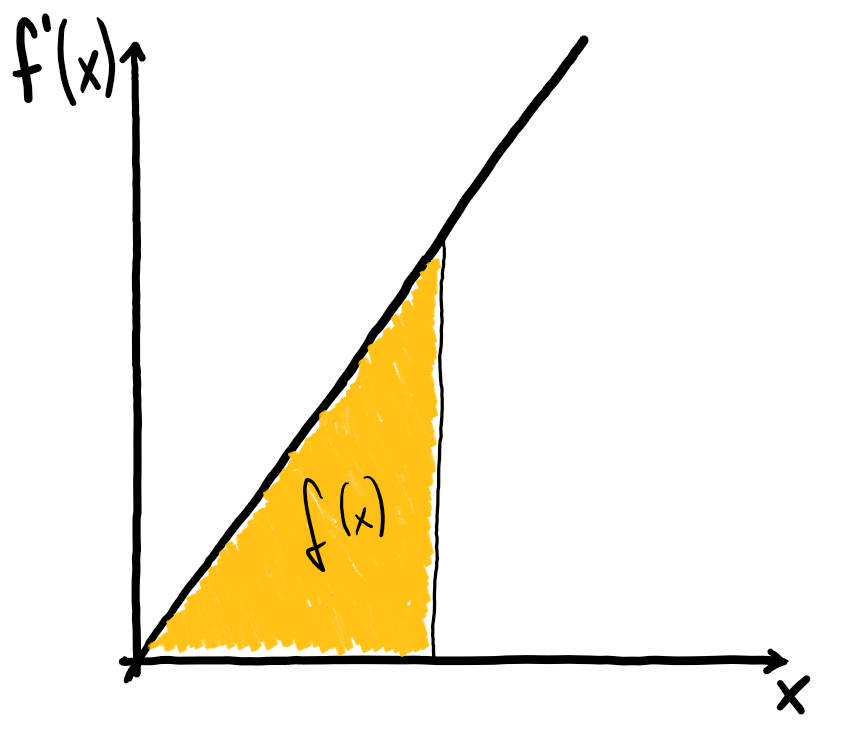
Das Integral beschreibt die Fläche unter dem Ableitungsgraphen $f’(x)$.
Da $f’(x)=2x$ ergibt sich abermals:
$$f(x)=\int 2x~\mathrm{d}x$$
# Zusammenfassung in einem Bild
$$ \begin{align*} \int \mathrm{d}f &= f(x)\\ \int f’(x)~\mathrm{d}x &= f(x) \end{align*} $$
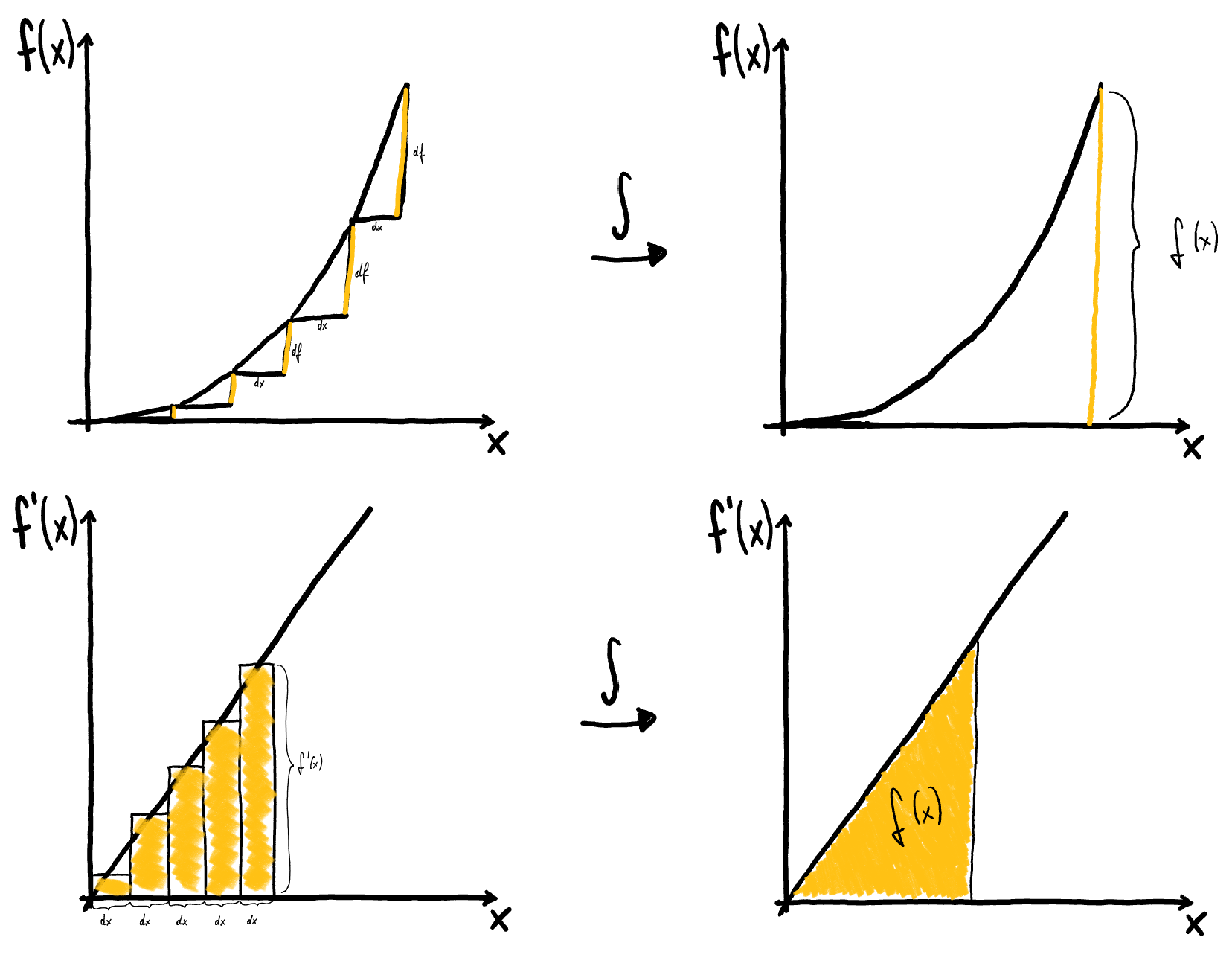
# Beweis
Der oben intuitiv veranschaulichte Zusammenhang zwischen Integral, Ableitung und Flächeninhalt ist so zentral für die Analysis, dass er den Namen Hauptsatz der Differential- und Integralrechnung trägt.
Als mathematischer Beweis für diesen Zusammenhang reichen obige Überlegungen jedoch nicht aus. Ein Beweis für den Hauptsatz der Differential- und Integralrechnung ist hier zu finden.